Energieentwertung

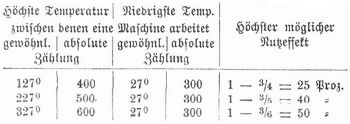
Energieentwertung (Dissipation, Degradation, Zerstreuung der Energie). Energie ist Arbeitsfähigkeit. Ob aber diese Arbeitsfähigkeit wirklich ausgenutzt werden kann, hängt im allgemeinen von besondern Bedingungen ab und damit der Wert der Energie, ähnlich wie auch der Wert des Geldes von besondern Umständen abhängig ist. Die Versuche, ein Perpetuum mobile zu konstruieren, sind gescheitert, obschon in der Wärme der Luft, der Erde, des Meerwassers ein praktisch unerschöpflicher Vorrat an Energie gegeben ist. Die Schwierigkeit liegt darin, daß diese Energie nicht ausgenutzt werden kann, sowenig wie die potentielle Energie eines auf dem Boden liegenden Steines, wenn kein Schacht vorhanden ist, in den er hinunterfallen kann. Nur wenn uns ein solcher Schacht für die Wärme zu Gebote stände, wohin wir dieselbe abfließen lassen könnten, wäre die Ausnutzung möglich. So könnten wir z. B. mittels einer Thermosäule, deren eines Ende sich im heißen Wüstensande der Sahara befindet, deren andres Ende in das Polareis versenkt ist, einen in die Leitung eingeschalteten Elektromotor unaufhörlich im Betrieb halten. Ohne Temperaturgefälle ist ein solches sogen. Perpetuum mobile zweiter Art unmöglich. Gleiches gilt für die Ausnutzung der Wärme durch Dampf- und Heißluftmaschinen, zu deren Betrieb notwendig außer der Wärmequelle ein Refrigerator (Kondensator, Kühlvorrichtung) gehört, der im einfachsten Falle durch die kühlere Umgebung dargestellt wird. Sadi Carnot, der zuerst (1824) diese Tatsache erkannte, verglich die mechanische Leistung der Wärme mit derjenigen des Wassers, das ebenfalls nur Arbeit leistet, wenn es von einem höhern zu einem tiefern Niveau herabsinkt. Während aber Carnot, noch auf dem Standpunkte der damals herrschenden Wärmestofftheorie, annahm, daß hierbei die Wärme ebenso wie das Wasser unvermindert zu dem tiefern Niveau herabgelange, machte Clausius (1850) darauf aufmerksam, daß gemäß dem von Robert Mayer (1842) entdeckten Satz von der Äquivalenz von Wärme und Arbeit (erster Hauptsatz der mechanischen Wärmetheorie) nur ein Teil der zugeführten Wärme als solche in den kältern Körper übergehen könne, wogegen der andre Teil, indem er eine ihm äquivalente Arbeitsmenge erzeugt, als Wärme verschwindet. Ist die obere Temperatur (Kesseltemperatur) nach absoluter Skala τ₁, die untere (Kondensatortemperatur) τ₂, die aufgenommene Wärmemenge Q₁ Kalorien, so wird im günstigsten Fall in Arbeit umgesetzt die Wärmemenge Q₁(τ₁-τ₂)/τ₁ Kalorien, d.h. der Wirkungsgrad einer solchen thermodynamischen Maschine, Thermosäule etc. ist höchstens τ₁-τ₂/τ₁ = 1-τ₂/τ₁, z. B.:

Die Nutzeffekte steigen zwar nur langsam mit wachsender Temperatur, immerhin aber ist die Wärme um so wertvoller, je höher sie temperiert ist. Vollständig in mechanische Energie würde Wärme umsetzbar sein in einer Maschine, die als Temperatur des Kühlers den absoluten Nullpunkt (-273°) hätte. Die von Carnot hervorgehobene Analogie tritt deutlich hervor, wenn man den Ausdruck für die Arbeit schreibt Q₁/τ₁.(τ₁-τ₂) und berücksichtigt, daß für einen vollkommenen Kreisprozeß (s. Druckkurven) Q₁/τ₁ = Q₂/τ₂, worin Q₂ die aus der Maschine austretende Wärme bezeichnet, d.h. daß dieses sogen. Wärmegewicht Q₁/τ₁ (auch reduzierter Wärmeinhalt oder Entropie) beim Durchgang der Wärme durch die Maschine ungeändert bleibt und nur gewissermaßen vom Wärmeniveau τ₁ auf das Niveau τ₂ herabsinkt. Für einen Wassermotor ist nämlich die Arbeitsleistung genau ebenso gleich Wassergewicht ✕ Wassergefälle, da dieses Produkt die verlorne potentielle Energie ergibt. Übrigens gilt auch für den Wassermotor ein dem Clausiusschen Satz ganz ähnlicher Satz, wenn man die potentielle Energie des Wassers nicht vom Erdboden aus rechnet, wo der Motor aufgestellt ist, sondern etwa vom Meeresspiegel oder vom Erdmittelpunkt. Beträgt die so gerechnete Energie des benutzten Wassers im obern Behälter U, im untern u und sind die Höhen der beiden Wasserspiegel H und h, so ist U:H = u:h oder (U-u)/U = (H-h)/H, woraus: U-u = U.(H-h)/H, d.h. der in Arbeit umgesetzte Teil der Gesamtenergie ist gleich dem Wassergefälle, dividiert durch den höchsten Wasserstand. Das aus der Maschine austretende Wärmegewicht Q₂/τ₂, das sich auf dem Niveau τ₂ befindet, hat keinen Wert mehr, da es sich unter den gegebenen Umständen nicht weiter in Arbeit umsetzen läßt, es ist entwertete Energie. Der verwandelbare Teil E = Q₁(τ₁-τ₂)/τ₁ der Gesamtenergie Q₁ wird auch freie Energie genannt, der Rest τ₂.Q₂τ₂ gebundene Energie. Man kann also schreiben Q₁ = E + τ₂S, worin S = Q₂/τ₂ = Q₁/τ₁ die Entropie bedeutet. Anstatt als Summe zweier Glieder kann man die Energie auch als Produkt zweier Faktoren darstellen, denn es ist Q₁ = τ₁.Q₁/τ₁ = τ₁.S, oder die Energie ist das Produkt der absinkenden Temperatur mit der Entropie. Der erste Faktor wird auch Intensitätsfaktor, der zweite Kapazitäts- oder Extensitätsfaktor genannt. Der erste hat stets das Bestreben abzunehmen, der zweite zuzunehmen. Die obigen Formeln ergeben sich aus dem von Clausius aufgestellten zweiten Hauptsatz der Thermodynamik, daß Wärme niemals von selbst von niederer zu höherer Temperatur übergeht. Unmittelbar klar ist dies für die Wärmeleitung, da stets die Wärme den kältern Stellen zustrebt, also der Intensitätsfaktor kleiner wird, während die Entropie sich vergrößert, da Q₁/τ₂ > Q₁/τ₁ insofern τ₂ < τ₁. Gleiches gilt für alle andern nicht umkehrbaren Vorgänge, die Entropie strebt stets einem Maximum zu, nur bei sogen. isentropischen (falls sie umkehrbar sind, adiabatischen) Prozessen bleibt sie konstant, Abnahme ist in keinem Falle möglich. In andrer Weise kann dasselbe ausgedrückt werden, indem man sagt, die freie Energie strebt einem Minimum zu. Sobald dieses erreicht ist, ist der Vorgang beendigt, es tritt Gleichgewicht ein. Bei Verwertung des Satzes ist zu berücksichtigen, daß Umwandlung von Wärme in mechanische Arbeit nicht nur möglich ist, wenn eine Temperaturdifferenz vorliegt, sondern auch wenn Druckdifferenz zur Verfügung steht (wie beim Druckluftmotor) oder chemische Affinität (wie z. B. bei galvanischen Elementen, die bei der Stromerzeugung sich abkühlen, oder bei sogen. endothermen chemischen Reaktionen, die unter Bindung von Wärme verlaufen). Aus diesem Grunde sind die Begriffe thermodynamisches Potential und chemisches Potential eingeführt worden, die den Begriff der freien Energie in dieser Hinsicht ergänzen. Die genaue Ermittelung des Wertes der freien Energie ist von größter Wichtigkeit zur Vorausberechnung des Verlaufs physikalischer und chemischer Vorgänge sowie zur Auffindung gesetzmäßiger Beziehungen zwischen den in Betracht kommenden Größen. So läßt sich z. B. hiernach die Änderung von Schmelz- oder Umwandlungstemperatur bei Änderung des Druckes, die Abhängigkeit der Löslichkeit von der Druckänderung, die Temperaturänderung eines elastisch gespannten Drahtes u. dgl. berechnen. Aber auch die Tatsache, daß bei der Umwandlung von Wärme in Bewegungsenergie, elektrische Energie, Strahlung etc. stets ein Teil der Energie unverwertbar übrigbleibt, während jene Energieformen mit Leichtigkeit vollkommen in Wärme übergehen, führt zu wichtigen Folgerungen, die zuerst von W. Thomson (1851) gezogen worden sind. Alle Energieformen müssen nämlich schließlich in die mindestwertige Energieform der Wärme übergehen; auch diese wird ihre Temperaturdifferenzen ausgleichen, dann hört aller Energieumsatz auf (Tod des Universums). Steht aber der Welt dieses Ende bevor, so kann sie auch nicht von Ewigkeit her bestehen, sondern sie muß vor einer endlichen, wenn auch noch so langen Zeit einen Anfang gehabt haben, als die E ein Minimum und die Temperaturunterschiede am größten waren; denn bestünde sie seit unendlich langer Zeit, so müßte der Umwandlungsprozeß bereits abgelaufen und sener Endzustand starren Todes und lautloser Ruhe jetzt schon eingetreten sein. Diese aus dem Begriff der E. gezogenen Folgerungen, die dem Weltall ein so trauriges Schicksal in Aussicht stellen, haben begreiflicherweise manchen Widerspruch hervorgerufen (vgl. Caspari, Die Thomsonsche Hypothese von der endlichen Temperaturausgleichung im Weltall, Stuttg. 1874). Rankine nahm an, daß an der Grenze des von Äther erfüllten Weltraumes, hinter dem sich ein absolut leerer Raum befinden sollte, eine vollständige Zurückwerfung der strahlenden Wärme stattfinde, und Reuschle machte unter Zustimmung Robert Mayers geltend, daß durch das Zusammenstürzen von Sonnen Kräfte entfesselt werden, welche die zerstäubten Massen in den weiten Weltraum hinausschleudern und ihre träge Zusammenballung verhindern. Man hat auch versucht, die Richtigkeit des zweiten Hauptsatzes überhaupt anzuzweifeln. So wachsen z. B. die Pflanzen bei verhältnismäßig niedriger Lufttemperatur, und doch kann man durch ihr Verbrennen hohe Hitzegrade erhalten, die Wärme scheint also von selbst auf höheie Temperatur gekommen zu sein; Tiere und Menschen, die sich von den Pflanzen nähren. vermögen Arbeitsleistungen zu vollbringen, die sich nicht ergeben aus der Verbrennungswärme der Nahrung und der geringen Temperaturdifferenz zwischen Körper und Umgebung. Dabei wird aber übersehen, daß die Energie den Pflanzen als Sonnenlicht zukommt, d.h. von einer Energiequelle sehr hoher Temperatur. Auch der Einwand, daß wir z. B. eine Heißluftmaschine bei einer Temperaturdifferenz von etwa 100° betreiben und den Strom einer durch sie betätigten Dynamomaschine benutzen können, den Kohlenfaden einer Glühlampe auf sehr hohe Temperatur zu bringen, ist leicht zu widerlegen, da die in der Glühlampe auftretende Wärme keineswegs »von selbst«,. d.h. ohne Kompensation, die hohe Temperatur angenommen hat, sondern gleichzeitig der weitaus größere Teil der dem Motor zugeleiteten Wärmeenergie auf niedrigere Temperatur gesunken ist.

Ebensowenig beweist die Tatsache, daß wir z. B. mit einer gegebenen Menge komprimierter Luft auf Kosten der Wärme der Umgebung einen Druckluftmotor mit Dynamomaschine treiben oder durch Auflösen von salpetersaurem Ammoniak in Wasser Kälte oder durch Absorption von Wasserdampf in Natronlauge Wärme erzeugen und die Temperaturdifferenz zum Betrieb einer thermodynamischen Maschine oder Thermosäule verwenden und auf diese Weise die Glühlampe speisen, d.h. Wärme von hoher Temperatur scheinbar ohne Kompensation erzeugen können, etwas gegen den zweiten Hauptsatz, da sich auf solche Art ein Perpetuum mobile nur herstellen ließe durch Wiederkomprimieren der Luft, bez. Wiedereindampfen der Salzlösung oder Lauge, wobei eben eine weit größere Wärmemenge auf niedrigeres Niveau sinten muß. Bisher unerklärt ist aber die Tatsache, daß ein radioaktiver Körper (s. Becquerelstrahlen) sich durch seine eigne Strahlung sogar recht erheblich zu erwärmen vermag.