- Ellipse
Ellipse (griech.), in der Grammatik Auslassung eines zur Vollständigkeit der Rede notwendigen, aber durch den grammatischen Zusammenhang leicht zu ergänzenden Satzteils, bildet sich leicht beim erregten Redner, wird aber auch in schriftlichen Darstellungen mit der Absicht angewendet, das Wesentliche des Gedankens schärfer heraustreten zu lassen, indem das minder Bedeutsame unausgesprochen bleibt. Vgl. Aposiopesis.
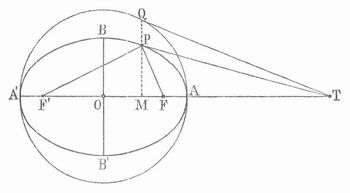
In der Geometrie ist E. eine zur Klasse der Kegelschnitte (s. d.) gehörige ebene Kurve, die durch zwei Punkte F, F´, die sogen. Brennpunkte, und durch eine Strecke von gegebener Länge 28 bestimmt ist und aus allen Punkten P besteht, bei denen die Summe PF + PF´ ihrer Entfernungen von den bei den Brennpunkten gleich 26 ist (s. Figur).
F P und F´ P nennt man die Radienvektoren von P. Da in dem Dreieck P F F´ die Summe der beiden Seiten P F, P F´ größer ist als die dritte Seite F F´´, so muß die Entfernung F F´ = 2e der Brennpunkte kleiner sein als 2a; man findet dann, daß die E. eine geschlossene, ganz im Endlichen liegende Kurve ist, die in ihrem Innern F und F´ enthält. Die Mitte O von F F´ heißt der Mittelpunkt der E., und ihre Entfernung e von F und F´ die lineare Exzentrizität, die Zahl e/a = ε, die immer kleiner als 1 ist, die numerische Exzentrizität, der Winkel φ, dessen Sinus gleich ε ist, der Exzentrizitätswinkel der E. Wird die Exzentrizität gleich Null, so verwandelt sich die E. in einen Kreis. Auf der Verlängerung der Geraden F F´ hat die E. zwei Punkte A, A´, für die OA = OA´ = a ist, auf der dazu senkrechten Geraden durch O hat sie zwei Punkte B, B´, für die OB = OB´ = √(a2e2) ist, was man gleich b setzt. Diese vier Punkte nennt man die Scheitel der E. A A´ und B B´ heißen die große und die kleine Achse der C. Durch a und b, also durch die Längen der halben großen und kleinen Achse, ist die E. offenbar ebenfalls bestimmt. Benutzt man die große und die kleine Achse als x-Achse und y-Achse eines rechtwinkligen Koordinatensystems (s. d.), so besteht zwischen den Koordinaten: OM = x und MP = y eines beliebigen Punktes P der E. die Gleichung x2/a2 +y2/b2 = 1. Beschreibt man um O mit dem Halbmesser OA = a einen Kreis, und fällt man von P auf die große Achse das Lot PM, dessen Verlängerung über P hinaus diesen Kreis in Q trifft, so verhält sich MP zu MQ wie b zu a. Zieht man in Q die Tangente an den Kreis, die auf OQ senkrecht steht, und trifft diese die große Achse in T, so ist TP die Tangente der E. in Punkt P. Noch einfacher erhält man die Tangente in P auf Grund des Satzes, daß die Normale von P, die in P auf der Tangente senkrecht steht, den Winkel zwischen den beiden Radienvektoren P F und P F´ halbiert. Der Flächeninhalt der E. ist a b π (über. π vgl. Kreis). Die E. ist von Wichtigkeit, weil die Planeten Ellipsen beschreiben, in deren einem Brennpunkte die Sonne steht. Vgl. Kegelschnitte, Planeten und Keplersches Problem.
http://www.zeno.org/Meyers-1905. 1905–1909.