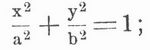Ellipsenzirkel

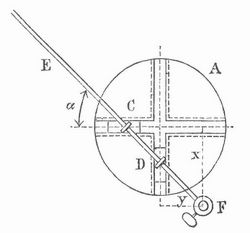
Ellipsenzirkel (Ellipsograph), Instrument zum Zeichnen von Ellipsen, besteht gewöhnlich aus einer Platte A (s. Abbildung), deren Mitte im Zentrum der Ellipse festgestellt wird. Die Platte hat zwei sich rechtwinklig schneidende Nuten, in denen die Schieber C und D sich bewegen, die mit der Stange EF durch Zapfen verbunden sind. Diese erhält dadurch eine zwangläufige Bewegung, bei der jeder Punkt der Stange eine Ellipse beschreibt. Ist CF = a, DF = b, so ist

und mithin

dies ist die Gleichung der Ellipse, bezogen auf ihre Hauptachsen; ein in F befestigter Zeichenstift beschreibt also eine Ellipse. Dabei ist die Entfernung der Punkte CD gleich der Differenz der beiden Halbachsen a und b einzustellen. Bei dem E. von Barocius (1586) wird eine mit einem Zeichenstift versehene Gerade um eine feste Achse herumgeführt und beschreibt dabei einen Kegelmantel, dessen Durchschnitt mit der Ebene des Papiers eine Ellipse ergibt.

Ellipsenzirkel.

Ohne Instrument zeichnet man eine Ellipse, wenn man in den beiden Brennpunkten die Enden eines Fadens befestigt, den Faden mit einem Zeichenstift spannt und diesen herumführt. Vgl. Fischer, Beiträge zur Geschichte, Theorie und Praxis der Zeicheninstrumente, insbes. der Ellipsographen (in Dinglers »Polytechn. Journal«, 1835); Rittershaus in den »Verhandlungen des Vereins zur Beförderung des Gewerbfleißes«, 1874.