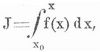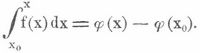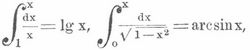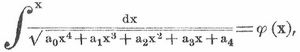Integralrechnung

Integralrechnung, die notwendige Ergänzung zur Differentialrechnung (s. d.). Während diese zu einer gegebenen Funktion den Differentialquotienten finden lehrt, besteht die Hauptaufgabe der I. darin, die Funktion zu finden, deren Differentialquotient gleich einer gegebenen Funktion ist. Wenn also f(x) eine gegebene Funktion ist, so sucht die I. eine solche Funktion F(x), daß d F/dx oder F'(x) = f(x) wird.

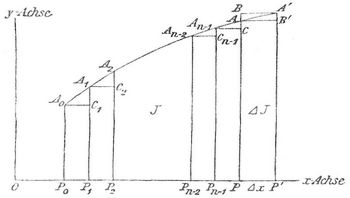
Eine Funktion von der verlangten Art kann man leicht angeben. Setzt man nämlich y = f(x) und deutet x und y als rechtwinklige Koordinaten (s. d.) in der Ebene, so stellt die Gleichung y = f(x) eine Kurve dar. Betrachtet man nun (s. Figur) den Flächeninhalt J, der begrenzt wird von dem Stücke der Kurve y = f(x), das liegt zwischen dem festen Punkte A₀ mit den Koordinaten x₀, y₀ = f(x₀), und dem veränderlichen Punkte A mit den Koordinaten x, y = f(x), ferner von den durch A₀ und A gezogenen Parallelen A₀P₀ und AP zur y-Achse und endlich von dem Stück P₀P der x-Achse, so ist J augenscheinlich durch die Abszisse OP = x des Punktes A bestimmt und ändert sich mit dieser, ist also eine Funktion von x. Läßt man jetzt x um PP´ = Δx wachsen, so wächst J um das Flächenstück PP'A'A = ΔJ, das zwischenden beiden Rechtecken PP'B'A und PP'A'B enthalten ist. Diese haben beide die Grundlinie Δx und der Reihe nach die Höhen PA = y = f(x) und PB = P'A' = f(x+Δx) = f(x)+Δf(x) (vgl. Differentialrechnung), ihre Flächeninhalte sind daher f(x) Δx und [f(x)+Δf(x)] Δx. Da ΔJ zwischen diesen beiden Grenzen liegt, so liegt ΔJ/Δx zwischen den Grenzen f(x) und f(x)+Δf(x). Lassen wir jetzt Δx immer kleiner werden und sich der Null nähern, so nähert sich auch Δf(x) immer mehr der Null und die beiden Grenzen, zwischen denen ΔJ/Δx eingeschlossen ist, kommen einander immer näher, um für Δx = 0 zusammenzufallen, während ΔJ/Δx selbst dem Grenzwerte dJ/dx zustrebt. Demnach ist J eine solche Funktion von x, daß dJ/dx = f(x) wird. Um diese Funktion zu berechnen, teilen wir das Intervall P₀P = x-x₀ in n gleiche Teile P₀P₁ = P₁P₂ = ... P_n-1P=1/n(x-x₀), errichten in den Teilpunkten P₁, P₂, ... auf der x-Achse die Senkrechten P₁A₁,P₂A₂, ... bis zur Kurve hin und fällen von A₀, A₁, ... aus die Lote A₀C₁, A₁C₂ ..., A_n-1C auf diese Senkrechten. So entstehen lauter kleine Rechtecke P₀P₁C₁A₀, P₁P₂C₂A₁, ... P_n-1PCA_n-1, die zusammengenommen kleiner sind als J. Ihre Grundlinien sind alle gleich 1/n(x-x₀)und ihre Höhen sind die Ordinaten der Punkte A₀, A₁, ...A_n-1. Da die Abszissen dieser Punkte die Werte x₀, x₀+1/n(x-x₀), x₀+2/n(x-x₀), ..., x₀+(n-1)/n(x-x₀) haben, so sind die Ordinaten gleich den zugehörigen Werten von f(x) und man findet:

wo das Summenzeichen ∑ bedeutet, daß für k der Reihe nach die Zahlen 0, 1, 2, ... n-1 zu setzen sind, und wo h die Summe der kleinen Dreiecke A₀C₁A₁, A₁C₂A₂, ..., A_n-1CA bedeutet, in denen jedesmal eine Seite ein Stück A₀A₁, A₁A₂, ... unsrer Kurve ist. Aber diese Dreiecke sind offenbar kleiner als die Rechtecke, die entstehen, wenn man von A₁, A₂, ..., A_n-1, A der Reihe nach auf die Verlängerungen von P₀A₀, P₁A₁, ..., P_n-1A_n-1 Lote fällt. Diese Rechtecke haben alle dieselbe Grundlinie 1/n(x-x₀), und die Summe ihrer Höhen ist gleich PA-P₀A₀ = f(x)-f(x₀), folglich ist die Summe ihrer Flächeninhalte = 1/n(x-x₀) (f[x]-f[x₀]) und h ist sicher kleiner als dieser Ausdruck. Lassen wir jetzt die ganze Zahl n immer größer und größer werden, so wird der letzte Ausdruck und somit auch h immer kleiner und kommt der Null beliebig nahe, demnach ist J der Grenzwert, dem sich die Summe S immer mehr nähert, wenn n über alle Grenzen wächst oder unendlich wird, in Zeichen:

(Über das Zeichen lim vgl. Grenze, S. 280.) Man schreibt hierfür bequemer:

gelesen Integral von x₀ bis x über f(x) dx; das Integralzeichen ∫ ist hier aus dem Anfangsbuchstaben S des Wortes Summe entstanden, und man hat sich unter dx den Ausdruck 1/n(x-x₀) für ein überaus großes n vorzustellen und gewissermaßen die Summe aller Produkte f(x)dx zu bilden, die man erhält, wenn man für x nach und nach alle zwischen x₀ und x liegenden Zahlen setzt. Der gefundene Ausdruck für J heißt ein bestimmtes Integral, x₀ seine untere, x seine obere Grenze. Er ist, wie wir wissen, eine Funktion von x, deren Differentialquotient gleich f(x) ist. Die allgemeinste Funktion dieser Art erhält man, wenn man zu J eine ganz beliebige, sogen. willkürliche Konstante, die Integrationskonstante, hinzufügt. Die Funktion F(x), für die F'(x) = f(x) ist, ist daher nur bis auf eine willkürliche Konstante bestimmt und hat die Form. J+C, wo die Konstante C ganz willkürlich ist. Um F(x) vollständig bestimmen zu können, muß man noch den Wert kennen, den F(x) für irgend einen Wert von x, etwa für x = x₀, haben soll; soll F(x₀) = a werden, so ergibt sich, da J für x = x₀ offenbar verschwindet, F(x) = J+a. Das sogen. unbestimmte Integral von f(x), dessen Zeichen ∫f(x)dx ohne Angabe von Grenzen ist, bedeutet eine ganz beliebige Funktion von x, deren Differentialquotient gleich f(x) ist. Kennt man, wie es oft vorkommt, zufällig schon eine Funktion φ(x), für die φ'(x) = f(x) ist, so ist ∫f(x)dx = φ(x)+C, dagegen

Während man den Differentialquotienten f´(x) einer Funktion f(x), deren Ausdruck gegeben ist, stets nach bestimmten Regeln berechnen kann, läßt sich das Integral der Funktion nur in den einfachsten Fällen durch bekannte Funktionen ausdrücken oder, wie man sagt, in endlicher geschlossener Form angeben, vielmehr ist es im allgemeinen bloß durch einen solchen Grenzwert wie den für J erhaltenen darstellbar. Die Betrachtung der Integrale bekannter Funktionen ist daher das hauptsächlichste Hilfsmittel zur Gewinnung neuer Funktionen geworden. Auch verschiedene schon bekannte Funktionen lassen sich in besonders einfacher Weise durch Integrale darstellen; z. B. ist

wo lg x der sogen. natürliche Logarithmus (s. d.) mit der Basis e = 2,7182818 ... und arc sin x die inverse Funktion (s. d.) zu sin x ist, d. h., arc sin x = y ist die Auflösung der Gleichung x = sin y nach y. Bei dem letzten Integral steht unter dem Integralzeichen im Nenner die Quadratwurzel aus einem Ausdruck vom zweiten Grade in x. Ersetzt man diesen Ausdruck durch einen vom vierten Grade, so erhält man ein elliptisches Integral:

so genannt, weil man auf ähnliche Integrale zuerst bei Berechnung der Bogenlänge der Ellipse gestoßen ist. Viele merkwürdige Eigenschaften dieser Integrale hat schon Euler entdeckt, aber es war Abel und Jacobi vorbehalten, die wichtigsten zu bemerken. Indem sie nämlich φ(x) = u setzten und sich diese Gleichung nach x aufgelöst dachten: x = ψ(u), erkannten sie, daß ψ(u) eine doppeltperiodische Funktion ist, denn es gibt zwei Größen: w₁ = α+βi, w₂ = γ+δi (α, β, γ, δ sind reelle Zahlen, i die Quadratwurzel aus -1 und αδ-βγ ist von Null verschieden), die so beschaffen sind, daß ψ(u) seinen Wert nicht ändert, wenn man das Argument u um w₁ oder um w₂ vermehrt, es besteht also für jeden Wert von u die Gleichung ψ(u+w₁) = ψ(u+w₂) = ψ(u). Wie also die trigonometrischen Funktionen sin x, cos x etc. (s. Trigonometrie) eine Periode besitzen, da sie ungeändert bleiben, wenn man den betreffenden Winkel um 360° oder das Argument x um 2.7 vermehrt, so haben diese neuen, die sogen. elliptischen Funktionen zwei Perioden. Hyperelliptische Intregale nennt man solche, bei denen unter der Quadratwurzel ein Ausdruck von höherm als dem vierten Grade steht und Abelsche Integrale (nach dem Norweger Abel, s. d.) alle die von der Form ∫f(x)dx, wo f(x) eine beliebige algebraische Funktion von x ist; auf Grund eines allgemeinen und höchst merkwürdigen Satzes, den Abel über diese Integrale aufgestellt hat (Abelsches Theorem), haben diese Integrale ebenso wie die elliptischen unter den Händen von Jacobi, Riemann, Weierstraß u. a. zu neuen Funktionen, den hyperelliptischen und den Abelschen Funktionen, geführt. Die Integrale dienen besonders zur Berechnung des Flächeninhaltes und der Bogenlänge ebener Kurven, ferner kann man auch den von einer krummen Fläche begrenzten Rauminhalt und die zugehörige Oberfläche durch sogen. mehrfache Integrale ausdrücken. Man kann endlich auch die Fundamentalaufgabe der I. verallgemeinern, indem man, statt eine Funktion zu suchen, deren Ableitung gegeben ist, verlangt, daß zwischen der unabhängigen Veränderlichen x, der gesuchten Funktion und deren Ableitungen beliebig hoher Ordnung eine Gleichung von gegebener Form bestehen soll, und man kann entsprechende Aufgaben für Funktionen mehrerer Veränderlicher stellen. Man gelangt jedoch so zu einem Teil der I., der jetzt als Theorie der Differentialgleichungen (s. d.) ein selbständiges, sich unausgesetzt erweiterndes Gebiet bildet.

Einzelne besondere Integrale hat schon Archimedes berechnet, natürlich ohne den allgemeinen Begriff des Integrals zu haben. Als allgemeine Methode stammt die I. von Newton und Leibniz (letzterer hat auch das Zeichen ∫ eingeführt) ebenso wie die Differentialrechnung (s. d., dort auch Literaturangaben).