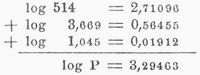Logarithmus

Logarithmus (griech., »Verhältniszahl«) einer Zahl b in bezug auf die Basis oder Grundzahl a nennt man den Exponenten β der Potenz (s. d.), auf die man die Basis a erheben muß, um die Zahl b zu erhalten; b selbst nennt man den zu dem L. gehörigen Numerus (lateinisches Wort für Zahl). Der L. von b mit der Basis a ist daher die Auflösung der Gleichung b = a^β nach β und man schreibt: β = ^alog b. Der Inbegriff aller Logarithmen in bezug auf eine bestimmte Basis a heißt das Logarithmen system mit der Basis a. Als Basis benutzt man immer eine positive Zahl a, und auch die Zahl b, deren L. genommen wird, setzt man als positiv voraus, weil nur in diesem Falle der L. reell (positiv oder negativ) wird (vgl. Exponentialfunktion). So ist ²log64 = 6, weil 2.2.2.2.2.2 = 2⁶ = 64 ist und ¹⁰log1000 = 3, weil 10³ = 1000. Praktische Verwendung finden eigentlich nur die Logarithmen mit der Basis 10, die dekadischen oder gemeinen (Briggschen) Logarithmen, die man meist mit log ohne Angabe der Basis bezeichnet und von denen im folgenden allein die Rede sein soll. Nach den allgemeinen Rechnungsregeln für Logarithmen (s. Exponentialfunktion) ist: log(b.c) = logb+logc; logb^k = klogb, wo b und c positiv, k aber beliebig positiv oder negativ sein kann. Also 1) der L. eines Produkts ist gleich der Summe der Logarithmen der einzelnen Faktoren. 2) Der L. einer Potenz ist gleich dem mit dem Exponenten multiplizierten L. der Grundzahl der Potenz. Hieraus folgt für k = -1:log1/b = -logb, also log^b/_c = logb-logc und für k = ¹/_n:logb^(1/n) = logⁿ√b = 1/nlogb. Mithin 3) der L. eines Bruches ist gleich dem L. des Zählers, vermindert um den des Nenners. 4) Der L. einer Wurzel ist gleich dem durch den Wurzelexponenten dividierten L. des Radikanden. Mit Hilfe der Logarithmen kann man daher die Multiplikation auf eine Addition, die Division auf eine Subtraktion, das Potenzieren auf eine Multiplikation, das Wurzelziehen auf eine Division zurückführen, vorausgesetzt, daß man zu jeder Zahl den zugehörigen L. und zu jedem L. den zugehörigen Numerus finden kann. Dieses wiederum wird durch eine Logarithmentafel ermöglicht, in der die gemeinen Logarithmen der Zahlen zusammengestellt sind. Die Logarithmen der Potenzen von 10 sind ohne weiteres angebbar, wie folgendes Schema zeigt:

Der L. jeder Zahl, die aus einer 1 und dahinter m Nullen besteht, ist also gleich m; der L. einer Zahl, die vor dem Komma eine Null, dahinter m Nullen und eine 1 enthält, ist gleich -m-1. Jede Zahl nun, die keine Potenz von 10 ist, kann durch Multiplikation (oder Division) mit einer geeigneten Potenz von 10 in eine zwischen 1 und 10 liegende Zahl verwandelt werden, deren L. zwischen 0 und 1 liegt und also ein echter Bruch ist, der, als Dezimalbruch geschrieben, vor dem Komma bloß eine Null enthält. Demnach setzt sich der L. einer beliebigen positiven Zahl b aus zwei Teilen zusammen: 1) aus einer bestimmten positiven oder negativen ganzen Zahl, der sogen. Charakteristik oder Kennziffer des L. von b, die nichts andres ist, als der L. der Potenz von 10, mit der man b dividieren muß, um eine zwischen 1 und 10 liegende Zahl b´ zu erhalten, und 2) aus einem positiven Dezimalbruch, der vor dem Komma eine Null hat, dem L. der Zahl b´. Die hinter dem Komma stehenden Ziffern dieses Dezimalbruches bilden die sogen. Mantisse des L. von b und zugleich die Mantisse der Logarithmen jeder Zahl, die aus b durch Multiplikation mit einer beliebigen Potenz von 10 entsteht. Demnach ist die Mantisse des L. einer im Dezimalsystem (s. d.) geschriebenen Zahl b vollständig bestimmt durch die Zifferngruppe, die man erhält, wenn man in dem Ausdruck für b, mit der ersten Ziffer, die keine Null ist, beginnend, von links nach rechts hin alle Ziffern aufschreibt bis zur letzten Ziffer, die keine Null ist. Die Stellung des Dezimalkommas und alle etwa links von dieser Zifferngruppe stehenden Nullen haben auf die Mantisse keinen Einfluß, ebenso alle Nullen, die etwa noch rechts von dieser Zifferngruppe stehen. So haben also die Zahlen 120, 500, 1205, 12,05, 0,0001205 alle dieselbe Mantisse. Der Logarithmentafel kann man nur die Mantisse des L. von b entnehmen, die Kennziffer aber findet man so: die zwischen 1 und 10 liegende Zahl b´, die aus b durch Multiplikation mit einer gewissen Potenz von 10 entsteht, ergibt sich, wenn man in b das Komma um eine gewisse Anzahl, etwa um m Stellen, nach rechts oder nach links so weit verschiebt, daß vor dem neuen Komma nur noch eine Ziffer, und zwar aus der Reihe 1, 2 ... 9, steht, die Kennziffer ist dann gleich +m oder gleich -m, je nachdem man das Komma nach links oder nach rechts verschoben hat. Z.B. besteht die Mantisse des L. von 514 aus den Zahlen 71096, also wird der L. von 514 gleich 2,71096, der von 5,14 gleich 0,71096, der von 0,00514 gleich 0,71096–3. Umgekehrt liefert die Mantisse eines L. sofort die vorhin besprochene Gruppe von Ziffern in dem zugehörigen Numerus, während die Kennziffer des L. die Stelle bestimmt, an die man in dem Numerus das Dezimalkomma zu setzen hat. Ist die Kennziffer m nicht negativ, so gehört das Komma hinter die m-te Ziffer jener Zifferngruppe, die fehlenden Ziffern sind durch Nullen zu ersetzen. Ist die Kennziffer negativ, gleich -m, wo m positiv ist, so hat man vor jene Zifferngruppe m+1 Nullen zu setzen und das Komma hinter die vorderste Null.

Da der L. einer Zahl im allgemeinen hinter dem Komma einen unendlichen Dezimalbruch enthält, so geben die Tafeln die Logarithmen nicht ganz genau, sondern nur bis zu einer bestimmten Dezimalstelle, man redet daher z. B. von fünfstelligen und siebenstelligen Logarithmentafeln. Ferner enthält jede Tafel nur die Mantissen für die Logarithmen aller Zahlen von 1 bis zu einer bestimmten Potenz von 10, eine fünfstellige Tafel z. B. geht von 1–10,000, liefert also nur die Logarithmen der Zahlen unmittelbar, bei denen die früher besprochene Zifferngruppe nichtmehr als vier Ziffern enthält. Besteht diese Zifferngruppe aus fünf und mehr Ziffern, so muß man den L. durch Interpolation (s. d.) finden. Sucht man umgekehrt zu einem L. den zugehörigen Numerus, so wird man auch nur ausnahmsweise gerade die Mantisse des gegebenen L. in der Tafel finden, man muß vielmehr meistens den gesuchten Numerus durch Interpolation bestimmen. Doch gibt es auch sogen. Tafeln von Antilogarithmen, aus denen man zu jeder Mantisse von z. B. fünf Dezimalen den zugehörigen Numerus unmittelbar entnehmen kann. Außer den Logarithmen der Zahlen enthalten die Logarithmentafeln durchweg auch die Logarithmen der trigonometrischen Funktionen, sinus, cosinus, tangens und cotangens (s. Trigonometrie).

Über die Einrichtung einer jeden Logarithmentafel, über das Rechnen mit Logarithmen und über das Interpolieren enthält gewöhnlich die Einleitung zur Tafel alles Nötige. Daher mögen hier nur noch einige Beispiele von Rechnungen mit L. folgen.

Um das Produkt P = 514. 3,669. 1,045 zu berechnen, hat man zu bilden:

also P = 1970,7. Der L. des Bruches B = 1,045:3,669 wird erhalten, indem man 0,56455 von 0,01912 abzieht; um hier wieder eine positive Mantisse zu erhalten, schreibt man den zweiten L. in der Form 1,01912–1, so daß die Subtraktion ausführbar wird und ergibt: logB = 0,45457–1, also wird B = 0,2848. Der L. von 2¹⁰ ist gleich 10. log2 = 10. 0,80103 = 3,01030, also 2¹⁰ = 1024. Der L. von ¹⁰√2 ist ¹/₁₀ log2 = 0,03010, also ¹⁰√2 = 1,0718. Hat man einen L. mit negativer Charakteristik durch eine ganze Zahl zu dividieren, so tut man gut, zu der Charakteristik so viele negative Einheiten hinzuzufügen, daß die Division ausgeht, vor dem Dezimalkomma muß man natürlich an Stelle der Null dieselbe Zahl von positiven Einheiten einsetzen. Z.B. ist der L. von 0,2 gleich 0,30103–1, um ¹⁰√0,2 zu berechnen, schreibt man diesen L. so: 9,30103–10 und findet: log ¹⁰√0,2 = 0,93010–1, also ¹⁰√0,2 = 0,85134. Um die Subtraktion eines L. zu vermeiden, benutzt man wohl das zu dem L. gehörige Komplement, d.h. die Zahl, die herauskommt, wenn man den L. von 0 abzieht; statt den L. zu subtrahieren, hat man dann das Komplement zu addieren. In dem zweiten Beispiel ist das Komplement des L. 0,56455 gleich 0,43545–1, was zu 0,01912 addiert wieder 0,45457–1 ergibt.

Früher benutzte man in der Regel siebenstellige Logarithmentafeln, auch in der Schule, da sich aber herausgestellt hat, daß die fünfstelligen Tafeln eine für alle praktischen Zwecke genügende Genauigkeit gewähren, verwendet man jetzt meist solche; die Physiker, Geodäten und Astronomen begnügen sich sogar meistens mit vierstelligen Tafeln und nur bei schwierigen Rechnungen, wo es auf ganz besondere Schärfe des Resultats ankommt, verwenden sie siebenstellige. Vierstellige Tafeln gibt es unter anderm von Henrici (Leipz. 1882) und Schülke (3. Aufl., das. 1900), fünfstellige von Hartenstein (das. 1897), von F. G. Gauß, solche, die zugleich Antilogarithmentafeln enthalten von H. Schubert (»Logarithmische Tafeln und Gegentafeln«, Leipz. 1897). Unter den siebenstelligen sind am bekanntesten die von Vega, später bearbeitet von Bremiker (75. Aufl. von Tietjen, Berl. 1894), ferner die von Schlömilch und von Bruhns. Über den Grad der Genauigkeit des Rechnens mit L. s. Lüroth, Vorlesungen über numerisches Rechnen (Leipz. 1900).

Während für das praktische Rechnen nur die gemeinen Logarithmen in Betracht kommen, versteht man in der höhern Mathematik unter dem L. einer Zahl durchweg den natürlichen oder hyperbolischen L. mit der Basis e (s. Exponentialfunktion). Man findet den gemeinen L. einer Zahl, wenn man den natürlichen L. mit 0,4342945 dem gemeinen L. von e multipliziert; diese Zahl heißt der Modul der gemeinen Logarithmen. Umgekehrt ist der natürliche L. einer Zahl gleich dem gemeinen multipliziert mit 2,3025851, dem natürlichen L. von 10.

Einem besondern Zwecke dienen die Additions- und Subtraktionslogarithmen, mit Hilfe deren man aus loga und logb den L. von a+b und von a-b bequemer finden kann, als es bei Benutzung der gewöhnlichen Logarithmentafeln möglich wäre. Sie sind 1803 von dem Italiener Leonelli veröffentlicht, aber erst 1812 durch Gauß allgemein bekannt geworden, daher nennt man sie auch Gaußische Logarithmen. Heutzutage findet man sie in jeder Logarithmentafel. – Das Rechnen mit Logarithmen hat zuerst John Napier (Neper) bekannt gemacht (1614), nach ihm heißen die natürlichen Logarithmen oft auch Nepersche. Doch hat nach dem Zeugnis Keplers der Schweizer Jobst Bürgi schon vor Neper mit Logarithmen gerechnet. Briggs machte 1615 Neper den Vorschlag, 10 zur Basis zu wählen, daher der Name Briggsche Logarithmen. Die ursprünglich sehr mühsame Berechnung der Logarithmen wurde später mit Hilfe der Differentialrechnung durch Ausstellung bequemer Reihenentwickelungen für die Logarithmen sehr vereinfacht. Vgl. M. Cantor, Vorlesungen über Geschichte der Mathematik, Bd. 2 (2. Aufl., Leipz. 1900); Kewitsch in der »Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht«, Bd. 27 (das. 1896); Tropfke, Geschichte der Elementarmathematik, Bd. 2 (das. 1903).