Addition

Addition (Summation, lat.), die erste der vier Spezies oder Hauptrechnungsarten der Arithmetik. Sie lehrt, mehrere gegebene Zahlen, die Summanden (Addenden, Posten), zueinander addieren, d.h. eine neue Zahl, ihre Summe, bilden, die ebensoviel Einheiten enthält wie die gegebenen Zahlen zusammen. Das Zeichen für die A. ist +, gelesen plus; z. B. wird die Summe von 12 und 17 geschrieben: 12+17 und ist gleich 29, kürzer: 12+17 = 29. Für die A. gilt das kommutative Gesetz, d.h. die einzelnen Summanden oder Glieder einer Summe können beliebig untereinander vertauscht werden, ohne daß sich der Wert der Summe ändert, z. B. 3+5+7 = 7+3+5 = 15. Ferner gilt das assoziative Gesetz, d.h. man kann beliebig viele der Summanden zu einer Teilsumme zusammenfassen, dann von den noch übrigen Summanden wieder beliebig viele zu einer Teilsumme u.s.f., die Summe der so entstehenden Teilsummen ist stets gleich der Summe der ursprünglichen Summanden. Z.B. ist 3+5+7+8 = 23, anderseits 3+7 = 10, 5+8 = 13 und 10+13 wieder = 23. Will man mehrere Summanden zu einer Teilsumme zusammenfassen, so schließt man ihre Summe in Klammern ein, z. B. 3+5+7+8 = (3+5) + (7+8) = (3+7) + (5+8); das assoziative Gesetz sagt daher aus, daß bei Bildung einer Summe das Setzen oder Weglassen von Klammern ohne Einfluß auf das Ergebnis ist. Will man prüfen, ob man die Summe einer größern Anzahl von Summanden richtig gebildet hat, so wiederholt man die A., nachdem man die Zahlen anders angeordnet hat, oder man faßt erst einzelne der Summanden zu Teilsummen zusammen und addiert dann diese Teilsummen, oder man wendet die Neunerprobe an, die freilich auch keine unbedingte Sicherheit gewährt (s. Neun und Elf). Vgl. Krönig, Neue Methode zur Vermeidung von Rechenfehlern (Berl. 1855).

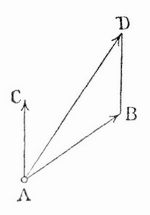
Ursprünglich werden bei der A. alle Summanden als positiv vorausgesetzt, man kann aber auch den Begriff der A. so verallgemeinern, daß man negative Summanden zuläßt, vgl. Negative Zahlen. Die Geometrie kennt eine A. der geraden Linien. Man denkt sich dabei die gerade Linie ihrer Länge und Richtung nach gegeben und betrachtet zwei solche gerade Linien (Strecken oder Vektoren) als gleich, wenn sie gleiche Länge und gleiche Richtung haben. Zwei solche Strecken AB und AC (s. Figur) addiert man, indem an den Endpunkt B der einen AB eine Gerade BD setzt, die nach Größe und Richtung mit der andern AC übereinstimmt; AD ist dann die geometrische Summe von AB und AC.