- Hypérbel
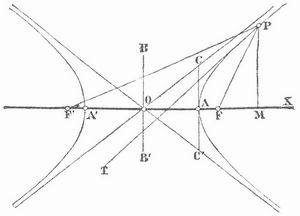
Hypérbel (v. griech. hyperbole, »Überschuß«), in der Geometrie eine zur Klasse der Kegelschnitte (s. d.) gehörige Kurve, die durch zwei feste Punkte F und F' (s. Figur), die sogen. Brennpunkte, und durch eine Gerade von gegebener Länge 20. bestimmt ist, und zwar ist für jeden ihrer Punkte P die Differenz seiner Entfernungen von den Brennpunkten gleich 23. Die Verbindungslinie F F' der Brennpunkte heißt die Hauptachse der H., die Mitte O von FF' ihr Mittelpunkt, die auf FF' in O senkrecht stehende Gerade BB' die Nebenachse. Die H. besteht aus zwei getrennten, sich ins Unendliche erstreckenden, zur Nebenachse symmetrischen Zweigen oder Ästen, von denen jeder wieder zur Hauptachse symmetrisch ist; für jeden Punkt P des einen Astes ist F'P-FP = 2a, für jeden Punkt P des andern Astes: FP-F'P = 2a. Die Geraden F'P und FP nennt man die Radienvektoren (Leitstrahlen) von P. Auf der Hauptachse liegen zwei Punkte A und A' der H., die von O die Entfernung a haben und Scheitel heißen, auf der Nebenachse liegt kein Punkt der H. Da in dem Dreieck F'PF die Differenz der beiden Seiten F'P, FP kleiner ist als die dritte FF' = 2e, so ist a kleiner als e, die Zahl e = e/a ist daher größer als l und heißt die numerische Exzentrizität, während e selbst die lineare Exzentrizität genannt wird. Setzt man b = √(e2-a2) und benutzt die Hauptachse zur x-Achse eines rechtwinkligen Koordinatensystems (s. Koordinaten), die Nebenachse zur y-Achse, so wird die Gleichung der H. x2/a2-y2/b2 = 1.
Die Tangente PT der H. im Punkt P halbiert den Winkel zwischen den Leitstrahlen F'P und FP. Die H. besitzt zwei Asymptoten, die durch den Mittelpunkt O gehen, d. h. zwei gerade Linien OC und OC´, die, verlängert, der H. immer näher und näher kommen, ohne sie jemals zu erreichen. Die Punkte CC' findet man, wenn man auf AA' in A die Senkrechte CC' errichtet und AC = AC' = b macht. Ist a = b, so stehen die Asymptoten aufeinander senkrecht, und die H. heißt gleichseitig. Vgl. Kegelschnitte.
In der Rhetorik und Poetik heißt H. die rednerische, bez. dichterische Übertreibung, d. h. die Charakterisierung eines Gegenstandes durch einen über das wirkliche oder mögliche Maß hinausgehenden Ausdruck. Die H. ist entweder ernst gemeint oder komisch; sie soll je nachdem die Bedeutung des Objekts steigern oder es in komische Beleuchtung rücken. Am häufigsten findet sie sich bei orientalischen Dichtern, bei Calderon, Shakespeare, Schiller, Victor Hugo, ebenso bei unsern Kraftdramatikern von Lenz und Klinger bis Hebbel. Antike Dichter und Schriftsteller sind damit sparsam, auch Goethe wendet sie selten an. Zahlreiche Beispiele komischer Hyperbeln geben Shakespeare, Jean Paul u. a. (z. B. bei Shakespeare: »Dein Kopf steht so wacklig auf dünnen Schultern, daß ein verliebtes Milchmädchen ihn herunterseufzen kann«).
http://www.zeno.org/Meyers-1905. 1905–1909.