- Ellipsoïd
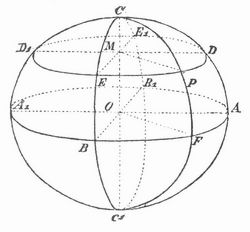
Ellipsoïd (griech., »ellipsenähnlich«), eine geschlossene krumme Fläche, ungefähr wie die Oberfläche eines Eies, wird folgendermaßen erhalten: man denke sich von einem Punkt O (s. Figur), dem Mittelpunkt, ausgehend drei gerade, zueinander senkrechte Linien und auf der ersten, die in der Papierebene liegt, nach beiden Seiten hin die Länge OA = OA1 = a, auf der zweiten, zur Papierebene senkrechten die Strecke OB = OB1 = b, auf der dritten, wieder in der Papierebene liegenden die Strecke OC = OC1 = c abgetragen. Die drei mit den Achsen A1 A und B1 B, A1 A und C1 C, B1 B und C1 C konstruierten Ellipsen bilden dann die Hauptschnitte des Ellipsoids, die Achsen selbst die Achsen des Ellipsoids; wenn sie alle drei verschieden sind, so ist das E. dreiachsig. Man denke sich jetzt die durch A A1, und B B1, gehende Ebene so verschoben, daß sie immer senkrecht zu C1 C bleibt; sie mag dann C1 C in M, die Ellipse ACA1 C1, in D und D1, die Ellipse BCB1 C1, in E und E1 schneiden. Mit den Linien D1 D und E1 E als Achsen konstruiert man wieder eine Ellipse und denkt sich diese Konstruktion für alle Lagen des Punktes M von C1 bis C ausgeführt. Die Fläche, auf der die so gewonnenen Ellipsen DED1 E1 sämtlich liegen, ist bann das dreiachsige E. Statt dessen kann man sich auch eine Ebene denken, die sich um die Achse C1 C dreht; ist F der Punkt, in dem sie bei irgend einer ihrer Lagen die Ellipse ABA1 B1 schneidet, so liegt auch die mit den Halbachsen OC und OF konstruierte Ellipse auf der Fläche.
Sind die beiden größern Halbachsen gleich groß, a = b > c, so ist die Fläche ein abgeplattetes Rotationsellipsoid, das durch Umdrehung der Ellipse A C A1 C1 um ihre kleine Achse C C1 entsteht. Die Oberfläche unsrer Erde bildet annähernd ein E. dieser Art; die Meridiane sind die kongruenten Ellipsen CAC1, CFC1 etc., der Kreis ABA1 B1 ist der Äquator, und die auf C C1, senkrechten ebenen Schnitte wie DED1 E1 sind ebenfalls Kreise (die Parallelkreise). Sind aber die beiden kleinern Halbachsen gleich, b = c < a, so erhält man ein gestrecktes Rotationsellipsoid, das entsteht, wenn sich die Ellipse ACA1 C1 um ihre große Achse AA1 dreht; in diesem sind alle Schnitte senkrecht zu A1 A Kreise. Ein E. mit drei gleichen Achsen ist eine Kugel. Der Rauminhalt des dreiachsigen Ellipsoids ist 4/3 abcπ (π = 3,1416; vgl. Kreis). Das E. gehört zu den Flächen zweiten Grades, weil es von einer Geraden in nicht mehr als zwei Punkten geschnitten werden kann; von einer Ebene wird es entweder in einer Ellipse oder in einem Kreise geschnitten. Seine Gleichung, bezogen auf die Achsen der Hauptschnitte als Koordinatenachsen, ist
http://www.zeno.org/Meyers-1905. 1905–1909.