- Elektrische Schwingungen
Elektrische Schwingungen, das durch die Selbstinduktion veranlaßte Hin- und Herströmen der Elektrizität in einem Leiter. E. S. treten auf bei der Entladung eines Kondensators, z. B. einer Leidener Flasche (Feddersen, 1858). Wird eine weite U-förmige Röhre halb mit Wasser gefüllt und etwa durch Saugen an einem Schenkel vorübergehend eine Niveaudifferenz erzeugt, so hört beim Zurücksinken des Wassers die Strömung nicht auf, wenn die Niveaudifferenz gleich Null geworden ist, denn infolge der Trägheit sucht das Wasser seine Bewegung fortzusetzen; aus dem Schenkel, in dem es höher stand, strömt also mehr heraus, als dem Niveauüberschuß entspricht, und in den andern fließt mehr hinein, als ursprünglich durch Saugen daraus herausgezogen war. Und geradeso wie ein gewöhnliches Pendel kommt das Wasser zur Ruhe, wenn es bet dieser Rückströmung die gleiche Höhe erreicht hat wie anfänglich, und pendelt dann wieder zurück. Infolge der Reibung werden allmählich die Schwingungen schwächer (Dämpfung) und hören schließlich ganz auf, um so eher, je enger die Röhre, d.h. je größer der Reibungswiderstand. Ganz ebenso pendelt die Elektrizität in dem Schließungsdraht eines Kondensators hin und her und die Schwingungen erlöschen um so rascher, je größer dessen Widerstand. Die bei der Entladung von dem einen Beleg zum andern strömende Elektrizität ruft nämlich durch Selbstinduktion (s. Elektrische Induktion, S. 624) im Schließungsdraht einen gleichgerichteten Extrastrom hervor, der bewirkt, daß aus der positiven Belegung mehr Elektrizität herausströmt, als der positiven Spannung entspricht, und in die negative mehr hinein, als nötig wäre, den Spannungsunterschied auszugleichen, der also den Kondensator entgegengesetzt ladet und dadurch eine abermalige Entladung in entgegengesetzter Richtung veranlaßt etc., so daß während der kurzen Dauer eines Entladungsfunkens in demselben eine große Anzahl solcher Hin- und Hergänge oder e. S. stattfinden. Die Schwingungsdauer T ist von der Kapazität C und dem Selbstinduktionskoeffizienten L der Leitung abhängig (T = 2π√(CL), entsprechend der Gleichung zπL-1/(zπC) = 0) und kann z. B. durch Betrachtung des Funkens in einem rotierenden Spiegel gemessen werden, wobei man statt eines in die Breite gezogenen Funkens deren eine große Anzahl in gleichen Abständen sieht, ähnlich wie bei Betrachtung einer schwingenden Flamme (s. Manometrische Flammen). Durch Wahl sehr kleiner Werte von C und L kann die Schwingungsdauer ungemein klein, die Schwingungszahl oder Polwechselzahl also ungeheuer groß werden. Hertz, der zuerst derartige Hochfrequenzströme erzeugte durch Entladungen zwischen kleinen Konduktoren, erhielt bereits Schwingungszahlen von der Ordnung 1 Milliarde in der Sekunde, später erhielt man mit kleinern Konduktoren bis hundertmal größere Werte, und aus den optischen Erscheinungen ist zu schließen, daß, wenn es möglich wäre, einzelne Atome als Konduktoren zu verwenden, die Schwingungszahl bis 100 und 1000 Billionen in der Sekunde getrieben werden könnte. Von der Polwechselzahl ist nun aber die Impedanz (der scheinbare Widerstand) eines Leiters abhängig (s. Elektrische Induktion, S. 624). Schon die relativ langsamen oszillierenden Ströme bei der Entladung von Leidener Flaschen durch einen kurzen dicken Draht (ohne erheblichen Widerstand) begegnen einem so hohen scheinbaren Widerstand in dem Drahte, daß infolge des dadurch bedingten großen Spannungsabfalls wegen der starken Krümmung der Oberfläche ähnlich wie aus Spitzen im Dunkeln Büschelentladungen von Anfang und Ende ausstrahlen oder in einer angelegten, durch eine Funkenstrecke unterbrochenen Nebenschlußleitung oder an den bei Ω-förmiger Krümmung (Priestleys Omega) einander nahekommenden Stellen Funken überspringen können. Man nennt diese Erscheinung Seitenentladung. Besonders auffällig zeigt sie sich, wenn man die Entladungen im Nebenschluß in eine Geißlersche Röhre übergehen läßt, oder wenn man (nach Tesla) die Unterbrechung durch eine Glühlampe überbrückt, die dabei zum Leuchten kommt. Außer der Induktanz zeigt sich auch eine Zunahme des Ohmschen Widerstandes, da solche rasche elektrische Oszillationen nicht in das Innere des Drahtes einzudringen vermögen (s. Energiestrom), wie namentlich Hertz mittels seines elektrodynamischen Käfigs, einer Röhre aus Drahtgeflecht, die einen von einer kleinen Funkenstrecke unterbrochenen Draht umgibt und mit ihm an den Enden leitend verbunden ist, bewiesen hat, insofern sich an der Unterbrechungsstelle, auch wenn diese sehr klein ist, nicht die geringsten Funken zeigen. Für den Ohmschen Widerstand ist deshalb nicht mehr der Querschnittsinhalt des Leiters maßgebend, sondern der Querschnittsumfang.
Selbstverständlich lassen sich mittels der Hochfrequenzströme auch ausgezeichnete Induktionswirkungen erhalten, da die induzierte elektromotorische Kraft bei einem Transformator der Polwechselzahl proportional ist (s. Elektrische Induktion, S. 624). Bereits die von Rieß hergestellten Induktionsscheiben, zwei isolierende Platten mit Drahtspiralen, durch deren eine die (oszillierenden) Entladungen einer Leidener Flasche geleitet werden, wobei an den Enden der induzierten Spirale so hohe Spannung auftritt, daß zwischen denselben zentimeterlange Funken überspringen, waren ein derartiger Hochfrequenztransformator; doch hat erst Hertz erkannt, daß seine Funktion auf der Bildung sehr rascher elektrischer Schwingungen beruht. Später hat Tesla den Apparat verbessert und zur bessern Isolation, d.h. zur Vermeidung der Ausströmung von Elektrizität aus den Drahtwindungen, in Form von Büschelentladungen ganz in Öl gesetzt (Öltransformator). – Bei kleinern neuern Apparaten verzichtet man auf Ölisolation und sucht, indem man für genügenden Abstand von Primär- und Sekundärspule sorgt, mit Luftisolation (Lufttransformatoren) auszukommen. Für die an der Sekundärspule auftretende Spannung ist übrigens bei einem Hochfrequenztransformator nicht wie bei einem gewöhnlichen Transformator für langsame elektrische Schwingungen (Wechselstrom) einfach das Übersetzungsverhältnis, d.h. das Verhältnis der Windungszahlen von Sekundär- und Primärspule, maßgebend, da natürlich die induzierten Ströme ebenfalls Hochfrequenzströme sind, also in der induzierten Spule einen außerordentlich hohen Widerstand erfahren. Nur wenn Resonanz besteht, d.h. wenn die nach der Formel T = 2π√(CL), berechnete Eigenschwingungsdauer für die Sekundärspule denselben Wert hat wie die der Primärspule, verschwindet der scheinbare Widerstand (s. Elektrische Induktion, S. 624), und man erhält derart hohe Spannungen, daß von den Enden der Spule, den Klemmschrauben, angesetzten Drähten, Konduktoren etc. die Elektrizität in Form ausgedehnter Büschel in den Raum gewissermaßen hinausstrahlt, richtiger ausströmt, indem sie die Luft in der Nähe elektrisch macht (ionisiert), welche Elektrisierung ihr natürlich bei jedem Polwechsel sofort wieder entzogen wird.
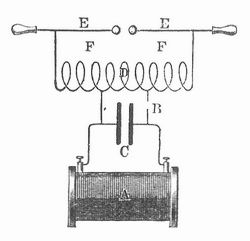
Ebenso wie bei einem gewöhnlichen Transformator kann auch bei einem Hochfrequenztransformator die Primärspule D (Fig. 1) einen Teil der sekundären F F bilden. Bei der dargestellten Anordnung wird der Kondensator C durch den Funkeninduktor A geladen und die Funkenstrecke B so gewählt, daß dort Entladungen eintreten.
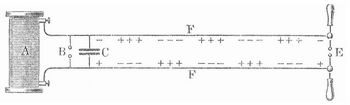
Bei jeder Entladung entstehen elektrische Schwingungen in D, die Eigenschwingungen in der Sekundärspule F F anregen und Entladungen mit großer Schlagweite zwischen den Elektroden EE veranlassen, vorausgesetzt, daß die beiden Spulen in Resonnanz stehen (aufeinander abgestimmt sind), was bei dieser Anordnung (nach Oudins Prinzip) dadurch erreicht werden kann, daß man die Zahl der als Primärspule benutzten Windungen durch Verschiebung eines Schleifkontakts so lange ändert, bis die Schlagweite ein Maximum erreicht. Die Spulen FF werden auch Multiplikationsspulen genannt, da sie die Spannung vervielfachen. Tesla erhielt auf diesem Wege Funken von mehreren Metern Länge. Einbringen eines Eisenkerns ist unnötig und schädlich, da der Magnetismus diesen raschen Schwingungen nicht zu folgen vermag, dagegen Wirbelströme nicht zu vermeiden sind. Es ist auch nicht nötig, daß die Spulen die Verlängerung der Primärspule bilden, da die von dieser ausgehenden rhythmischen elektrischen Störungen, von denen magnetische unzertrennlich sind, die Resonanzschwingungen bei beliebiger Lage anregen, und zwar nicht wie bei einem gewöhnlichen Transformator, bei dem in allen Windungen gleichzeitig Induktion eintritt, sondern derart, daß die Störung längs den Drähten der Spiralen mit der Geschwindigkeit von rund 3.108 m in der Sekunde fortschreitet. Diese Verhältnisse lassen sich am besten übersehen, wenn man statt der Spiralen geradlinig ausgestreckte Drähte verwendet, wie Fig. 2 andeutet.
Von jeder der beiden Platten des Kondensators C schreiten längs der Drähte F F elektrische Störungen entlang, ähnlich wie Seilwellen, so daß, wenn an diesen Drähten Elektroskope angehängt wären, dieselben nicht alle gleichzeitig in Tätigkeit treten würden, sondern zunächst die am Anfang, dann die weiter entfernten etc. und die Störung erst nach l/(3.108) Sekunden am Ende E anlangen würde, wenn l die Länge eines Drahtes in Metern bedeutet.
Da sich während des Fortschreitens der Störung der elektrische Zustand der Kondensatorplatten ändert, werden ferner, wie es die Zeichen in der Figur andeuten, an einzelnen Stellen die Elektroskope mit positiver Elektrizität divergieren, an andern mit negativer; es schreiten längs der Drähte elektrische Wellen fort, ganz ebenso wie bei Seilwellen die Teilchen sich abwechselnd nach der einen oder andern Seite (oben oder unten) bewegen. Ganz wie bei Seilwellen tritt ferner am Ende der Drähte bei E Reflexion der Wellen ein, und durch Übereinanderlagerung der ankommenden und reflektierten Wellen bilden sich stehende Wellen (s. Wellenbewegung), so daß an einzelnen Punkten, den Knoten, die Spannung beständig gleich Null bleibt, während sie an den Bäuchen zwischen positiven und negativen Werten hin und her schwankt. Bei hohen Spannungen sind diese stehenden Wellen im Dunkeln leicht zu erkennen, da an den Schwingungsbäuchen die Elektrizität in Form von Büschelentladungen an die benachbarten Luftschichten übergeht (bez. von diesen in den Draht zurückströmt), während die Knotenpunkte dunkel bleiben. Bei schwächern Spannungen kann man den Schwingungszustand in gleicher Weise sichtbar machen, wenn man nach Coolidge als primären Schwingungskreis einen Blondlotschen Oszillator verwendet, dessen Hälften zu einem Ring zusammengebogen sind und auf einen in geringem Abstand zusammen mit ihm in ein Ölbad eingesetzten gleich großen parallelen sekundären Ring einwirken läßt, der an einer Stelle aufgeschnitten ist und dort in die geradlinigeu Leiter ausläuft. Ferner kann man solche schwache elektrische Drahtwellen sichtbar machen, wenn man die Drähte durch eine evakuierte Röhre (Aronsröhre) führt, in der die Entladungen leichter erfolgen als in Luft von gewöhnlicher Dichte. Bei geringen Spannungen ist das Lechersche Verfahren von Vorteil, bei dem die Lage der Knoten dadurch ermittelt wird, daß das Aufl egen einer Brücke, d.h. die Herstellung einer leitenden Verbindung zwischen zwei gegenüberstehenden Knoten, da dieselben spannungsfrei sind, keinen Strom in der Brücke, somit auch keine Änderung der Entladungen in einer bei E angebrachten Vakuumröhre bedingen kann. Aus dem Abstand zweier Knotenpunkte ergibt sich die Wellenlänge λ, die doppelt so groß ist wie feuer, und hieraus die Fortpflanzungsgeschwindigkeit, da, wenn n Wellen in der Sekunde vom Kondensator ausgehen, die in dieser Zeit zurückgelegte Strecke, d.h. die Fortpflanzungsgeschwindigkeit v = nλ sein muß. So fand zuerst Hertz, daß v = 3.108 m = 300,000 km in der Sekunde ist. Die Geschwindigkeit ist übrigens, wie die Theorie lehrt, abhängig von den Eigenschaften des die Drähte umgebenden Mediums, insbes. deren Diëlektrizitätskonstante und magnetischer Permeabilität, so daß also der Knotenabstand ein andrer wird, wenn man die Drähte z. B. durch Petroleum statt durch Luft hindurchführt. Es lassen sich deshalb aus solchen Versuchen auch Schlüsse auf die Größe der beiden Konstanten ziehen. Setzt man v als bekannt voraus, so können die Versuche ferner dazu dienen, n, d.h. die Schwingungszahl der oszillatorischen Entladungen zu bestimmen, und, da diese selbst wieder von V und L abhängen, einen dieser beiden Werte, d.h. die Diëlektrizitätskonstante des Mediums zwischen den Kondensatorplatten oder die magnetische Permeabilität des den Entladungsdraht umgebenden Mediums.
Die Schwingungen in einem Hertzschen Oszillator können ebenso wie die auf dem Lecherschen Drahtsystem als stehende elektrische Wellen betrachtet werden, deren Schwingungsbäuche an den Enden sich befinden, ebenso wie bei einem in der Mitte eingeklemmten, durch Reiben in longitudinale Schwingungen versetzten elastischen Stab. Da nun die Entfernung zwischen zwei Schwingungsbäuchen gleich der halben Wellenlänge ist, muß die ganze Wellenlänge gleich dem doppelten der Länge l des Oszillators sein, somit die Schwingungsanzahl n = (3.108)/2l. (S. auch Energie und Elektrische Wellen.) Vgl. Hertz, Untersuchungen über die Ausbreitung der elektrischen Kraft (2. Aufl., Leipz. 1892); J. J. Thomson, Recent researches in electricity and magnetism (Lond. 1893); Drude, Physik des Äthers (Stuttg. 1894); Abraham, Die elektrischen Schwingungen um einen stabförmigen Leiter (Berl. 1897); Righi, Die Optik der elektrischen Schwingungen (deutsch, Leipz. 1898); Lecher, Über die Entdeckung der elektrischen Wellen durch Hertz (das. 1901); Braun, Drahtlose Telegraphie (das. 1901); Righi u. Dessau, Die Telegraphie ohne Draht (Braunschw. 1903).
http://www.zeno.org/Meyers-1905. 1905–1909.