Oberfranken

Oberfranken, Regierungsbezirk des Königreichs Bayern (s. Karte »Bayern, nördlicher Teil«), grenzt im N. an die thüringischen Staaten Reuß, Sachsen-Meiningen und Sachsen-Koburg, im W. an Unterfranken, im S. an Mittelfranken, im SO. an Oberpfalz, im Osten an Böhmen und Sachsen, besteht hauptsächlich aus dem ehemaligen Fürstentum Bayreuth im Osten und dem ehemaligen Hochstift Bamberg im W. und umfaßt 6999 qkm (127,12 QM.) mit (1905) 637,239 Einw. darunter (1900) 347,231 Evangelische, 256,917 Katholiken und 3322 Juden), 91 auf 1 qkm O. ist durchweg gebirgig, den Osten und Nordosten durchziehen das Fichtelgebirge und der Frankenwald, den Westen der höhlenreiche Frankenjura und der Ostabfall des Steigerwaldes. Hauptflüsse sind: der Main mit der Regnitz, in die hier der mit ihr parallel laufende Ludwigs- (Donau-Main-) Kanal mündet, die Saale und die Eger. Fruchtbare Gefilde enthält namentlich der Westen, daher hier auch der Ackerbau gegen den höher gelegenen, rauhern Osten überwiegt. Weinbau, vorzüglicher Gemüse-, Obst- und Gartenbau sind besonders in der Gegend um Bamberg zu finden; von Wichtigkeit ist dort auch der Hopfenbau. Im Osten des Landes, im Fichtelgebirge und Frankenkel versehen ist, und beschreibt zwischen den Ansatzstellen des Henkels um die Kugel herum eine geschlossene Linie, so wird die den Körper begrenzende Fläche noch nicht in zwei Teile zerlegt, weil die beiden Teile der Kugel durch die Oberfläche des Henkels verbunden sind; eine solche Fläche heißt zweifach zusammenhängend. Eine besonders fruchtbare Methode zur Untersuchung der Flächen rührt von Gauß her. Man betrachtet dabei die Fläche für sich allein, gar nicht als einen Bestandteil des Raumes, und zwar wird das ermöglicht durch Einführung eines Koordinatensystems auf der Fläche; man denkt sich nämlich auf der Fläche zwei Kurvenscharen (die sogen. Parameterlinien) derart, daß durch jeden Punkt der Fläche je eine Kurve der ersten und eine Kurve der zweiten Schar geht; jeder Punkt der Fläche ist dann vollständig bestimmt, wenn man angibt, welche Kurve der ersten und welche der zweiten Schar durch ihn geht.

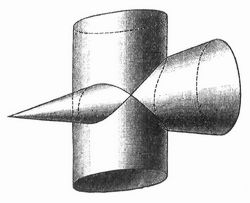
Ein solches System von Parameterlinien bilden z. B. auf der Erdoberfläche die Längen- und die Breitenkreise und auf einer beliebigen Fläche die Krümmungslinien (s. Indikatrix). Zwei verschiedene Flächen schneiden einander im allgemeinen in einer Kurve, ihrer Durchdringungskurve oder ihrem Schnitt. In der Figur ist der Schnitt zwischen einem Kreiskegel und einem Kreiszylinder dargestellt. Die ersten allgemeinen Untersuchungen über O. stammen von Euler, aber es waren besonders Monge durch seine »Application de l'analyse à la géométrie« (Par. 1809) und Gauß durch seine »Disquisitiones circa superficies curvas« (Götting. 1827; deutsch in »Ostwalds Klassikern«, Leipz. 1889), welche die Flächentheorie zu einer selbständigen Wissenschaft, dem Hauptgegenstande der heutigen Differentialgeometrie, erhoben. Zusammenfassende Werke über den Gegenstand sind: Darboux, Leçons sur la théorie générale des surfaces (Par. 1887–96, 4 Bde.); Bianchi, Vorlesungen über Differentialgeometrie (deutsch von Lukat, Leipz. 1899). Lehrbücher: Knoblauch, Einleitung in die allgemeine Theorie der krummen Flächen (Leipz. 1888); Scheffers, Einführung in die Theorie der Flächen (das. 1902); Stahl und Kommerell, Die Grundformeln der allgemeinen Flächentheorie (das. 1893). Seit Plücker und Kummer bedient man sich mit großem Vorteil zur Veranschaulichung von Flächen der Modelle, besonders solcher aus Gips; eine reichhaltige Sammlung von solchen erscheint im Verlag von Schilling (Halle a. S.), früher bei Brill (Darmstadt).