- Niveaulinien
Niveaulinien, bei der kartographischen Darstellung eines Geländes die Linien, die in diesem Gelände von den Punkten gleichen Niveaus, d.h. von den Punkten gleicher Höhe über dem Meeresspiegel gebildet werden. Indem man eine Anzahl solcher N. in die Karte einzeichnet, kann man die Erhebungen und Senkungen des Geländes zur Anschauung bringen.
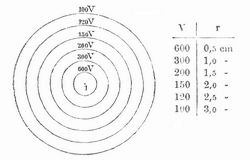
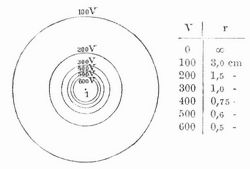
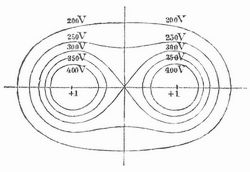
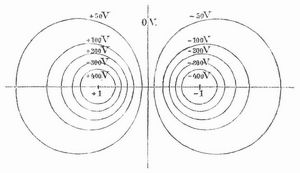
In der Potentialtheorie versteht man unter N. gewöhnlich ebene Schnitte von Niveauflächen (s. d.), und man bedient sich ihrer, um die von den wirkenden Massen ausgehende Kraft graphisch darzustellen. Die folgenden Beispiele beziehen sich auf Elektrizität und Magnetismus. Ist M ein mit einer elektrischen Einheit geladener Massenpunkt, d.h. also mit 300 Volt, so hat ein Punkt P in der Entfernung von r cm das Potential 300´r Volt. Beschreibt man um M Kreise mit den Radien 1 cm, 2 cm etc., so erhält man die N., die zu den Werten 300 Volt, 150 etc. des Potentials gehören (Fig. 1). In der Regel zeichnet man die N. so, daß die Differenz der zugehörigen Potentiale für je zwei Linien gleich ist. Soll diese z. B. 100 Volt betragen, so bestimmt man die zugehörigen r aus den Gleichungen 1/r1.300 = 100; 1/r2300 = 200 etc., also r1 = 3 cm; r2 = 1,5 etc. (Fig. 2). Sind zwei elektrische Massenpunkte vorhanden, beide mit den Ladungen +1, so ist das Potential eines Punktes P. der von den beiden Zentren die Entfernungen r und ρ hat, = (1/r+1/ρ) 300 Volt. Danach besteht für die Niveaulinie, die zu einem Potentiale von v Volt gehört, die Gleichung 1/r+1/ρ = v/300. aus der man beliebig viele zusammengehörige Paare r und p berechnen und damit den Verlauf der Niveaulinien ermitteln kann. Figur 3 zeigt die N. einiger Potentialwerte, wenn die Entfernung der beiden elektrisch geladenen Punkte 4 cm beträgt. Figur 4 bezieht sich auf den Fall, daß die beiden Zentren entgegengesetzte Ladungen +1 und -1 haben. Diese Zeichnungen können auch bezogen werden auf den Fall punktförmig gedachter Magnetpole. Die Zeichnung der elektrischen etc. Niveau- (und Kraft-) Linien wurde besonders durch Maxwell eingeführt. Vgl. »Höhenlinien« und Maxwell, Lehrbuch der Elektrizität u. des Magnetismus, Bd. 1 (deutsch von Weinstein, Berl. 1883); Hovestadt, Lehrbuch der angewandten Potenzialtheorie (Stuttgart 1890).
http://www.zeno.org/Meyers-1905. 1905–1909.