Parabel

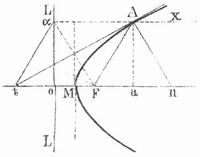
Parabel (v. griech. parabŏlē, »Anlegung«, übertragen: »Vergleichung«), in der Geometrie eine zur Klasse der Kegelschnitte gehörige Kurve, die durch einen festen Punkt F, den Brennpunkt, und durch eine feste Gerade L, die Leitlinie oder Direktrix, bestimmt ist. Ein Punkt A ist als Punkt der P. dadurch gekennzeichnet, daß sein Abstand AF von dem Brennpunkt F gleich ist dem Abstand A α von der Leitlinie L (s. Figur). Fällt man von F das Lot F o auf die Leitlinie, so ist die Mitte M von Fo ein Punkt der P., ihr Scheitel.

Die Strecke Fo bezeichnet man mit p und nennt sie den Parameter der P., die Gerade, in der Fo liegt, nennt man die Achse. Die zur Achse parallelen Geraden sind die Durchmesser. Fällt man von A das Lok Aa auf die Achse, macht Mt = Ma und zieht tA, so ist tA die Tangente der P. in A, noch einfacher findet man diese, indem man von A aus das Lot At auf Fα fällt. Die Tangente der P. in M (die Scheiteltangente) steht auf der Achse senkrecht. Benutzt man M als Anfangspunkt und die Achse als Abszissenachse eines rechtwinkligen Koordinatensystems, so besteht zwischen den rechtwinkligen Koordinaten Ma = x und aA = y von A die Gleichung: y² = 2px. Die Gerade FA heißt der Leitstrahl oder radius vector von A; errichtet man auf der Tangente in A die Senkrechte An (die Normale der P. im Punkt A) und zieht man durch A den Durchmesser Ax parallel zur Achse, so sind die Winkel xAn und FAn einander gleich. Denkt man sich daher einen Lichtstrahl, der parallel der Achse, von x kommend, die P. in A trifft und von dieser zurückgeworfen (reflektiert) wird, so wird dieser nach der Reflexion stets durch den Brennpunkt F gehen. Darauf beruht die Wichtigkeit der parabolischen Hohlspiegel; die spiegelnde Fläche eines solchen Spiegels wird erhalten, wenn man sich eine P. um ihre Achse gedreht denkt, er vereinigt alle der Achse parallelen Lichtstrahlen in dem Brennpunkt F. Die P. ist ferner von Bedeutung als die Bahn, die ein geworfener schwerer Körper im luftleeren Raum beschreibt; auch die Bahnen der meisten Kometen sind Parabeln.