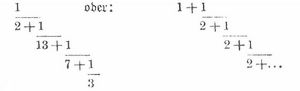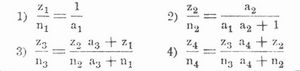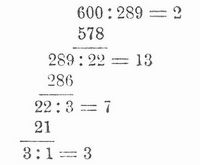- Kettenbruch
Kettenbruch (kontinuierlicher Bruch), ein Bruch, dessen Zähler eine ganze Zahl und dessen Nenner die Summe aus einer ganzen Zahl und einem Bruche von derselben Bildungsweise ist, z. B.:
Der erste K. ist endlich und hat einen rationalen Wert; der zweite, der nie abbricht, heißt unendlich und hat einen irrationalen Wert, nämlich. √2. Die Brüche 1/2, 1/13, 1/2, 1/3 im ersten und 1/2, 1/2, ...im zweiten Beispiele heißen Glieder des Kettenbruches. Haben alle Glieder den Zähler 1, wie im ersten Beispiele, so heißt der K. einfach. Bildet man aus einem einfachen K. nacheinander die Kettenbrüche, die entstehen, wenn man nur das erste, die zwei, drei... ersten Glieder beibehält, und berechnet man die Werte dieser sogen. Partialbrüche, so erhält man sogen. Näherungswerte für den ursprünglichen K. Diese Näherungswerte sind abwechselnd zu groß und zu klein, kommen aber dem wahren Werte des gegebenen Kettenbruches immer näher, weil die Näherungswerte ungerader Ordnung, also der erste, dritte,... abnehmen, die von gerader Ordnung aber, der zweite. vierte,... zunehmen. Sind a1, a2, a3 etc. die aufeinanderfolgenden Nenner der Glieder des einfachen Kettenbruches, die Teilnenner, so sind die Näherungswerte:
u. s. s. Demnach hat z. B. der erste der obigen Kettenbrüche die Näherungswerte:
deren letzter den wahren Wert des Kettenbruches angibt. Zwischen den Zählern und Nennern des (k-1)-ten und des k-ten Näherungswertes besteht die wichtige Beziehung:
aus der folgt, daß die Näherungswerte sämtlich reduzierte Brüche sind, d. h. Brüche, deren Zähler und Nenner keinen gemeinsamen Teiler haben. Ferner folgt daraus, daß die Differenz:
ist; sind nun die Teilnenner ak alle positiv, so werden die ganzen Zahlen n1, n2... der Reihe nach immer größer und diese Differenz mit wachsendem k immer kleiner, worin liegt, daß die Näherungswerte eines unendlichen einfachen Kettenbruches mit lauter positiven Teilnennern einer bestimmten endlichen Grenze zustreben, daß der K. konvergent (s. d.) ist. Die einfachen Kettenbrüche benutzt man namentlich, um für Brüche mit sehr großen Zählern und Nennern Näherungswerte zu finden, die in kleinern Zahlen ausgedrückt sind, dabei hat man zugleich den Vorteil, daß diese Näherungswerte, wie gesagt, reduzierte Brüche sind. Da der Wert eines einfachen Kettenbruches stets kleiner als 1 ist, so muß man, um eine Zahl in einen K. zu entwickeln, erst die Ganzen ab sondern und dann den übrigbleibenden echten Bruch in einen K. verwandeln. Zu dem Ende dividiere man mit dem Zähler des echten Bruches in den Nenner, dann mit dem Rest in den vorigen Divisor (den Zähler des echten Bruches) und fahre so fort, indem man immer mit dem jeweiligen Rest in den vorigen Divisor dividiert, bis die Rechnung ausgeht. Die Quotienten, die sich bei den einzelnen Divisionen ergeben, sind die Teilnenner des gesuchten Kettenbruches. Einen Dezimalbruch muß man erst als gemeinen Bruch schreiben, bevor man ihn in einen K. verwandelt. Z. B. ergibt die Verwandlung von 289/600 folgende Rechnung:
und man erhält so die Teilnenner des früher angegebenen Kettenbruches. Wegen der Gleichung (I) benutzt man die Kettenbrüche auch in der Zahlentheorie, um die ganzzahligen Lösungen x, y einer Gleichung von der Form ax+by = 1 zu finden, wo a und b ganze Zahlen sind, man braucht dazu nur den Bruch a/b in einen K. zu entwickeln, Zähler und Nenner des vorletzten Näherungswertes dieses Kettenbruches liefern dann sofort ein Wertepaar x, y. Endlich dienen die unendlichen Kettenbrüche in der Analysis zur Darstellung irrationaler Zahlen, ein Beispiel dafür ist der angegebene K. für (√2. –) Die Verwandlung eines gewöhnlichen Bruches in einen K. deckt sich mit Euklids Verfahren zur Aufsuchung des größten gemeinschaftlichen Teilers oder Faktors zweier ganzer Zahlen (vgl. Faktor), nur die Schreibung als K. ist modern. Der K. tritt zuerst bei Cataldi auf (um 1540–1626) und wird da zur Ausziehung von Quadratwurzeln benutzt. Der Name fractio continua, der dann mit K. übersetzt wurde, kommt zuerst bei Euler vor (1737). Näheres über die Kettenbrüche findet man in den Lehrbüchern der Arithmetik und Algebra.
http://www.zeno.org/Meyers-1905. 1905–1909.