- Ziffern
Ziffern (Zahlzeichen), schriftliche Zeichen zum Ausdruck der Zahlen. Ein sehr nahe liegendes Hilfsmittel besteht in der Benutzung der Buchstaben des Alphabets als Z., wie wir dies bei den allen Griechen seit dem 5. Jahrh. v. Chr. finden. Diese ergänzten zu dem Zweck ihr (ionisches) Alphabet durch 3 Episemen (Buchstaben eines ältern Alphabets), nämlich ς oder Vau, (
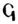 oder Koppa und
oder Koppa und 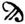 oder Sampi, die hinter ε, π und ω) gesetzt wurden. Die Buchstaben α, β, γ, δ, ε, ς, ζ, η, ϑ bedeuteten die Einer 1, 2,... 9, ferner ι, κ, λ, υ, ν, ξ, ο, π,
oder Sampi, die hinter ε, π und ω) gesetzt wurden. Die Buchstaben α, β, γ, δ, ε, ς, ζ, η, ϑ bedeuteten die Einer 1, 2,... 9, ferner ι, κ, λ, υ, ν, ξ, ο, π,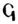 die Zehner 10, 20,... 90 und ρ, σ, τ, υ, φ, χ, ψ, ω,
die Zehner 10, 20,... 90 und ρ, σ, τ, υ, φ, χ, ψ, ω,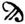 die Hunderte 100, 200,... 900. Abgesehen von der großen Menge der Zeichen, hatte dieses System den Mangel, daß es die Entstehung des Vielfachen von 10 oder 100 aus diesen Zahlen und einem andern Faktor verhüllte. Um größere Zahlen durch wenige Z. darzustellen, wendete man verschiedene Mittel an. Gewöhnlich benutzte man für 1,10,100,1000 etc., verschiedene Zeichen, die man so oft wiederholte wie nötig; damit aber der Wiederholungen nicht zu viele wurden, gab man auch den Zahlen 5,50,500 etc. eigne Zeichen. Hierher gehört das Ziffersystem, das auf ältern griechischen Inschriften im Gebrauch ist: die Einheit wird mit einem Strich I bezeichnet; für 5, 10, 100, 1000 und 10,000 werden die Anfangsbuchstaben der Zahlwörter Pente, Deka, Hekaton, Chilioi, Myrioi benutzt; 50,500,5000 und 50,000 werden durch das Zeichen für 5 ausgedrückt, in das man die Zeichen für 10,100,1000 und 10,000 einschreibt. Es ist also I = 1, II = 2, Γ = 5, Γ III = 8, Δ = 10, ΔΔΔ = 30, ΔΔΔ II = 32, Γ = 50, H = 100, Γ = 500, X = 1000, M = 10,000. Bei Anwendung dieses Verfahrens schreibt man die höhern Stufenzahlen vor den niedern, also die Hunderte vor den Zehnern und diese vor den Einern; doch findet sich hiervon im Ziffersystem der Römer eine Ausnahme. Dieses hat die einfachen Zeichen I = 1, V = 5, X = 10, L = 50, C = 100, IƆ oder D = 500, CIƆ oder M = 1000; es ist also MDCCCLXXVIII = 1878. Man setzt aber auch die niedere Zahl links vor die höhere, um anzudeuten, daß sie von der höhern abzuziehen ist: IX = 9, XL = 40, XC = 90. Abweichend sind im römischen Ziffersystem: IƆƆ = 5000, CCIƆƆ = 10,000, CCIƆƆƆ = 50,000, CCCIƆƆƆ = 100,000, CCCCIƆƆƆƆ = 1 Mill. Ein andres Verfahren besteht darin, durch unter oder über die Z. gesetzte Zeichen den Zahlwerk zu vervielfachen. Dies findet Anwendung bei den spätern griechischen Buchstabenziffern für die Tausende, die durch dieselben Buchstaben wie die Einer, nur mit untergesetzten Strichen bezeichnet werden: ᾳ = 1000, β = 2000 bis ι = 10,000 oder eine Myriade. Nach einem dritten Verfahren wird der Wert durch vorangestellte Ziffern vervielfacht. So bezeichnen z. B. Pappos und Diophant 2 Myriaden = 20,000 durch βMυ, während αMυβ = 10,002 ist. Weiter ist zu erwähnen die schon im Mittelalter in Europa vorkommende Schreibweise in Spalten (Kolumnen), die mit I, X, C etc. überschrieben sind, und in die man die Anzahl der Einer, Zehner, Hunderte etc. einträgt; sind für eine Stufe keine Einheiten vorhanden, so bleibt die betreffende Spalte leer; vgl. nebenstehend die Schreibweise von 542, 540, 502 und 42.
die Hunderte 100, 200,... 900. Abgesehen von der großen Menge der Zeichen, hatte dieses System den Mangel, daß es die Entstehung des Vielfachen von 10 oder 100 aus diesen Zahlen und einem andern Faktor verhüllte. Um größere Zahlen durch wenige Z. darzustellen, wendete man verschiedene Mittel an. Gewöhnlich benutzte man für 1,10,100,1000 etc., verschiedene Zeichen, die man so oft wiederholte wie nötig; damit aber der Wiederholungen nicht zu viele wurden, gab man auch den Zahlen 5,50,500 etc. eigne Zeichen. Hierher gehört das Ziffersystem, das auf ältern griechischen Inschriften im Gebrauch ist: die Einheit wird mit einem Strich I bezeichnet; für 5, 10, 100, 1000 und 10,000 werden die Anfangsbuchstaben der Zahlwörter Pente, Deka, Hekaton, Chilioi, Myrioi benutzt; 50,500,5000 und 50,000 werden durch das Zeichen für 5 ausgedrückt, in das man die Zeichen für 10,100,1000 und 10,000 einschreibt. Es ist also I = 1, II = 2, Γ = 5, Γ III = 8, Δ = 10, ΔΔΔ = 30, ΔΔΔ II = 32, Γ = 50, H = 100, Γ = 500, X = 1000, M = 10,000. Bei Anwendung dieses Verfahrens schreibt man die höhern Stufenzahlen vor den niedern, also die Hunderte vor den Zehnern und diese vor den Einern; doch findet sich hiervon im Ziffersystem der Römer eine Ausnahme. Dieses hat die einfachen Zeichen I = 1, V = 5, X = 10, L = 50, C = 100, IƆ oder D = 500, CIƆ oder M = 1000; es ist also MDCCCLXXVIII = 1878. Man setzt aber auch die niedere Zahl links vor die höhere, um anzudeuten, daß sie von der höhern abzuziehen ist: IX = 9, XL = 40, XC = 90. Abweichend sind im römischen Ziffersystem: IƆƆ = 5000, CCIƆƆ = 10,000, CCIƆƆƆ = 50,000, CCCIƆƆƆ = 100,000, CCCCIƆƆƆƆ = 1 Mill. Ein andres Verfahren besteht darin, durch unter oder über die Z. gesetzte Zeichen den Zahlwerk zu vervielfachen. Dies findet Anwendung bei den spätern griechischen Buchstabenziffern für die Tausende, die durch dieselben Buchstaben wie die Einer, nur mit untergesetzten Strichen bezeichnet werden: ᾳ = 1000, β = 2000 bis ι = 10,000 oder eine Myriade. Nach einem dritten Verfahren wird der Wert durch vorangestellte Ziffern vervielfacht. So bezeichnen z. B. Pappos und Diophant 2 Myriaden = 20,000 durch βMυ, während αMυβ = 10,002 ist. Weiter ist zu erwähnen die schon im Mittelalter in Europa vorkommende Schreibweise in Spalten (Kolumnen), die mit I, X, C etc. überschrieben sind, und in die man die Anzahl der Einer, Zehner, Hunderte etc. einträgt; sind für eine Stufe keine Einheiten vorhanden, so bleibt die betreffende Spalte leer; vgl. nebenstehend die Schreibweise von 542, 540, 502 und 42.Man bedarf nur noch eines Zeichens für eine leere Stelle, der Null, um die Kolumnen entbehren zu können und die jetzt bei uns übliche Schreibweise zu erhalten, bei der jede Ziffer durch den Platz, den sie einnimmt, ihren Wert (Positions- oder Stellenwert) erhält. Dieses System nun, in dem sich jede beliebig große Zahl mittels der 10 Z. 0, 1, 2 etc. bis 9 ausdrücken läßt, stammt von den Indern her, bei denen es zuerst im 5. Jahrh. n. Chr. auftritt. Nach dem Abendland ist es von den Arabern gebracht worden, daher auch unsre Z. gewöhnlich »arabische« genannt werden. Diese Z., doch zum Teil in Formen, die beträchtlich von den jetzigen abweichen, und ohne die Null, findet man schon in Handschriften aus dem 11. und 12. Jahrh.; die Benutzung des Stellenwertes aber hat das christliche Abendland hauptsächlich durch den »Liber Abaci« (1202) des Pisaners Leonardo Fibonacci (s. d.) kennen gelernt. In Italien scheint das neue Ziffersystem schon im 13. Jahrh. von den Kaufleuten benutzt worden zu sein, aber noch im 15. Jahrh. findet man es in nicht mathematischen Schriften selten; allgemeiner werden die neuen Z. in Schrift und Druck erst seit Mitte des 16. Jahrh. Mit den Z. kam auch das arabische Wort für die Null, sifr, franz. zéro, zu uns, das, im Laufe der Zeit seine Bedeutung ändernd, in »Ziffer« übergegangen ist. Vgl. Treutlein, Geschichte unsrer Zahlzeichen (Karlsr. 1875); Weißenborn, Zur Geschichte der Einführung der jetzigen Z. in Europa durch Gerbert (Berl. 1892); Gundermann, Die Zahlzeichen (Gießen 1899); Tropfke, Geschichte der Elementarmathematik, Bd. 1 (Leipz. 1902); Mischke, Naturgeschichte der Z. (Brem. 1907).
http://www.zeno.org/Meyers-1905. 1905–1909.

