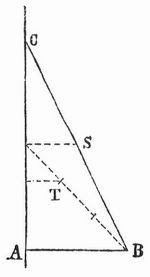
Baryzentrische Regel

Baryzentrische Regel

Baryzentrische Regel (zentrobarische, Guldinsche Regel), von dem Jesuiten Guldin in dem Werke »De centro gravitatis« (1635–41) angegebene, aber schon dem Pappos (s. d.) bekannte Regel zur Bestimmung des Rauminhaltes und der Oberfläche eines Umdrehungskörpers (vgl. Achse). Der Rauminhalt (die Oberfläche) des Körpers wird erhalten, wenn man den Inhalt des ebenen Flächenstücks (die Länge der ebenen Kurve), durch dessen (deren) Drehung der Körper (die Oberfläche) entsteht, mit der Länge des Weges multipliziert, den der Schwerpunkt des Flächenstücks (der Kurve) bei der Drehung zurücklegt. Dreht sich z. B. ein rechtwinkeliges Dreieck CBA (s. Figur) um die Kathete AC = h, so beschreibt die andre Kathete AB = r eine Kreisfläche und die Hypotenuse BC = s den Mantel eines geraden Kreiskegels. Die Fläche des Dreiecks ist 1/2 rh, ihr Schwerpunkt T liegt um 1/3 r von der Drehungsachse AC entfernt, beschreibt also bei der Drehung einen Kreis vom Halbmesser 1/3 r, die Länge seines Weges ist also = 2.1/3π (π = 3,14, s. Kreis), und der Rauminhalt des Kegels wird 1/2π.2/3π = 1/3r2hπ. Dagegen ist der Schwerpunkt S der Hypotenuse BC um 1/2r von der Achse entfernt und beschreibt bei der Drehung einen Weg 2.1/2rπ, so daß die Mantelfläche des Kegels = r. s.π ist. Andre Beispiele findet man in den Lehrbüchern der Stereometrie.

Tabelle

http://www.zeno.org/Meyers-1905. 1905–1909.

Игры ⚽ Нужно сделать НИР?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Baryzentrische Regeln — Rotationskörper werden in der Geometrie Körper genannt, die durch Rotation einer erzeugenden Kurve um eine Rotationsachse gebildet werden. Die Kurve liegt dabei in einer Ebene, und auch die Achse liegt in ebenderselben. Die Kurve schneidet die… …   Deutsch Wikipedia

  • Guldinsche Regel — Guldinsche Regel, baryzentrische Regel (benannt nach dem Jesuiten Paul Guldin, gest. 1643 in Graz), geometr. Regel zur Berechnung des Rauminhaltes und der Oberfläche von Rotationskörpern: 1) der Inhalt ist gleich der Fläche, durch deren Rotation… …   Kleines Konversations-Lexikon

  • Zentrobarische Regel — Zentrobarische Regel, s. Baryzentrische Regel …   Meyers Großes Konversations-Lexikon

  • Guldinsche Regel — Rotationskörper werden in der Geometrie Körper genannt, die durch Rotation einer erzeugenden Kurve um eine Rotationsachse gebildet werden. Die Kurve liegt dabei in einer Ebene, und auch die Achse liegt in ebenderselben. Die Kurve schneidet die… …   Deutsch Wikipedia

  • Zentrobarische Regel — Rotationskörper werden in der Geometrie Körper genannt, die durch Rotation einer erzeugenden Kurve um eine Rotationsachse gebildet werden. Die Kurve liegt dabei in einer Ebene, und auch die Achse liegt in ebenderselben. Die Kurve schneidet die… …   Deutsch Wikipedia

  • Baryzéntrum — (grch. lat.), Schwerpunkt. Baryzentrisch, auf den Schwerpunkt bezüglich. Baryzentrische Regel, s.v.w. Guldinsche Regel (s.d.) …   Kleines Konversations-Lexikon

  • Barycentrum — (griech. lat.), der Schwerpunkt; vgl. Baryzentrische Regel …   Meyers Großes Konversations-Lexikon

  • Guldin — Guldin, Paul (vor seinem Übertritt Habakuk), Mathematiker, geb. 12. Juni 1577 in St. Gallen, gest. 3. Nov. 1643 in Graz, erlernte die Goldschmiedekunst, trat 1597 in Freising zum Katholizismus über und dann zu München in den Jesuitenorden. In der …   Meyers Großes Konversations-Lexikon

  • Achsenkreuz — Zweidimensionale, kartesische Koordinaten zur Lokalisierung von Hydranten und Wasserabsperrhähnen. Ein Koordinatensystem (mathematisches Kürzel: KOS) dient der Positionsangabe von Punkten im Raum. Der Fachbegriff der Koordinate, in der Bedeutung… …   Deutsch Wikipedia

  • Koordinate — Zweidimensionale, kartesische Koordinaten zur Lokalisierung von Hydranten und Wasserabsperrhähnen. Ein Koordinatensystem (mathematisches Kürzel: KOS) dient der Positionsangabe von Punkten im Raum. Der Fachbegriff der Koordinate, in der Bedeutung… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”