- Schwerpunkt
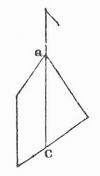
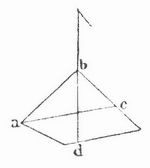
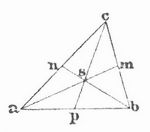
Schwerpunkt, der Angriffspunkt der Mittelkraft aus allen an den verschiedenen Teilchen eines Körpers angreifenden Schwerkräften. Da diese Kräfte lotrecht gerichtet und sonach unter sich parallel sind, so ist ihre Mittelkraft gleich ihrer Summe, d. h. gleich dem Gesamtgewicht des Körpers. Der S. ist daher derjenige Punkt, in dem das ganze Gewicht des Körpers vereinigt gedacht werden kann, und der unterstützt sein muß, wenn der Körper der Schwere gegenüber sein Gleichgewicht behaupten soll. Ein aufgehängter Körper befindet sich in festem Gleichgewicht, wenn der S. lotrecht unter dem Aufhängungspunkt liegt. Hängt man einen Körper mittels eines am Punkt a seines Umfanges befestigten Fadens auf (Fig. 1), so muß die Verlängerung a c des Fadens durch den S. gehen und stellt somit eine Schwerlinie des Körpers dar; hängt man nun den Körper an einem zweiten Punkt b (Fig. 2) auf, so muß der S. abermals in der Verlängerung des Fadens, nämlich auf der Schwerlinie bd, liegen; er liegt sonach im Durchschnittspunkt der Linien ac und bd. Bei Körpern von gleichartiger Masse und regelmäßiger Gestalt läßt sich der S. häufig durch einfache geometrische Betrachtungen auffinden. Der S. eines Dreiecks (Fig. 3) z. B. muß notwendig auf der Geraden liegen, die von einer Ecke c nach der Mitte p der Gegenseite geht; denn zu beiden Seiten dieser Linie ist die Masse des Dreiecks in gleicher Weise verteilt, und sie ist sonach eine Schwerlinie.
Zieht man daher von einer zweiten Ecke a aus noch eine solche Schwerlinie am, so ist ihr Durchschnittspunkt s der gesuchte S., durch den nun auch die dritte Schwerlinie bn gehen muß; dieser Punkt 8 liegt so, daß ps = 1/3pc ist. Den S. eines Vielecks findet man durch Zerlegung desselben in Dreiecke. Der S. einer Pyramide oder eines Kegels liegt auf der von der Spitze nach dem S. der Grundfläche gezogenen Linie um ein Viertel derselben von der Grundfläche entfernt. Bei Körpern, die einen Mittelpunkt besitzen, z. B. Kugel, Ellipsoid, ist derselbe zugleich S.; bei einem Zylinder mit parallelen Endflächen liegt der S. in der Mitte der Achse, bei einem Parallelepiped im Durchschnittspunkt der drei Diagonalen. Der S. eines Körpers liegt übrigens nicht immer innerhalb seiner Masse; bei einer Schale, Flasche z. B. liegt er in deren Hohlraum. Vgl. Erhaltung des Schwerpunktes.
http://www.zeno.org/Meyers-1905. 1905–1909.