- Hyperboloīd
Hyperboloīd (griech.), Fläche zweiter Ordnung wie das Ellipsoid (s. d.).
Am einfachsten ist das Rotationshyperboloid, das man erhält, wenn man sich eine Hyperbel (s. d.) um eine ihrer Achsen gedreht denkt; je nachdem man die Hauptachse oder die Nebenachse als Drehachse benutzt, erhält man ein zweischaliges oder einschaliges Rotationshyperboloid. Das einschalige wird von jeder zur Drehachse senkrechten Ebene in einem Kreise geschnitten, beim zweischaligen dagegen ist jeder zwischen den Scheiteln der erzeugenden Hyperbel liegende Punkt der Drehachse so beschaffen, daß eine durch ihn gehende, zur Drehachse senkrechte Ebene die Fläche gar nicht trifft, die beiden in den Scheiteln auf der Drehachse senkrecht stehenden Ebenen haben mit der Fläche nur diese Scheitel gemein, während alle andern auf der Drehachse senkrechten Ebenen gleichfalls Kreise ausschneiden.
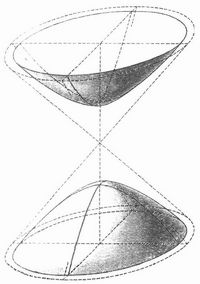
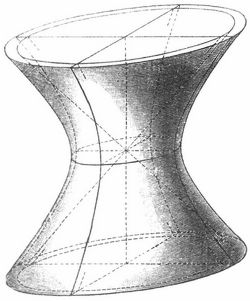
Denkt man sich ein Rotationshyperboloid so zusammengedrückt, daß aus den besprochenen Kreisen Ellipsen werden, so erhält man eine deutliche Vorstellung von dem allgemeinen, zweischaligen (Fig. 1) oder einschaligen H. (Fig. 2), die Gerade, die beim Rotationshyperboloid Drehachse war, heißt dann beim allgemeinen H. Hauptachse.
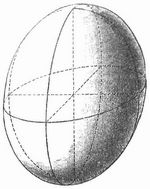
Das zweischalige H. ist in jedem seiner Punkte gekrümmt wie ein Ellipsoid (Fig. 3), das zweischalige dagegen ist in jedem Punkte sattelförmig gekrümmt.
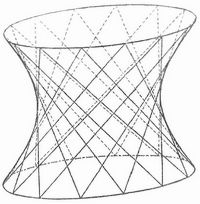
Beim einschaligen heißt die kleinste der Ellipsen, die von einer zur Hauptachse senkrechten Ebene ausgeschnitten wird (in Fig. 2 ist sie eingezeichnet an der Stelle, wo die Fläche am stärksten eingeschnürt ist), die Kehlellipse. Auf dem einschaligen H. gehen durch jeden Punkt zwei gerade Linien, die ganz auf der Fläche liegen, es gehört also zu den Geradlinigen Flächen (s. d.). Die auf der Fläche liegenden Geraden bilden zwei Scharen, die in Fig. 4 angedeutet sind. Das einschalige Rotationshyperboloid kann man auch dadurch erhalten, daß man sich eine Gerade um eine zu ihr windschiefe Achse gedreht denkt.
http://www.zeno.org/Meyers-1905. 1905–1909.