- Zykloïde
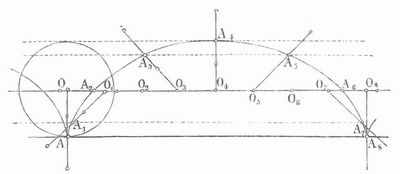
Zykloïde (griech., »Radlinie«), die ebene Kurve, die ein Punkt auf dem Umfang eines Kreises beschreibt, wenn dieser auf einer geraden Linie, der Grundlinie oder Basis, hinrollt, ohne zu gleiten. Ist A der Punkt, der die Z. beschreibt (Fig. 1, S. 1052), und O die Anfangslage des Kreismittelpunktes, so nimmt O, wenn 1/8, 2/8... des Kreisumfanges über die Basis hingerollt sind, der Reihe nach die Lagen O1, O2,... an und A die Lagen A1, A2,... Aus der Figur geht hervor, daß die Z. von A an in die Höhe steigt und bei A4 ihren höchsten Punkt erreicht, dann sinkt sie wieder, immer ihre hohle Seite der Basis zukehrend, und erreicht bei A8 die Basis wieder; die Strecke AA8 ist gleich dem Kreisumfang, also wenn r der Kreishalbmesser ist, gleich 2 r. r. In A8 beginnt ein neues Kurvenstück, das dem ersten gleich ist, und die ganze Z. besteht aus unendlich vielen solchen Stücken; wo zwei solcher Stücke zusammenstoßen, hat die Z. eine Spitze. Natürlich muß man sich die Z. von A aus auch nach links fortgesetzt denken. Der ganze Zykloidenbogen von A bis A8 hat die Länge 8 r, und der Flächenraum zwischen diesem Bogen und der Basis ist gleich 3r2π, also gleich der dreifachen Fläche des rollenden Kreises. Die Z. hat viele von Pascal, Huygens etc. entdeckte merkwürdige Eigenschaften. Sie ist Brachistochrone und zugleich Tautochrone oder Isochrone; hat man nämlich die Z. so gestellt, daß ihre Ebene lotrecht und die Basis wagerecht steht, daß sie aber selbst unterhalb der Basis liegt und ihre hohle Seite nach oben kehrt, so braucht ein schwerer Punkt, der längs der Z. herunterfällt, stets dieselbe Zeit, um nach dem tiefsten Punkte der Z. zu kommen, von welcher Stelle der Kurve aus er auch seine Bewegung beginnt. Genaueres über die Z. findet man in jedem Lehrbuche der Differentialrechnung und der analytischen Mechanik. Außer der bisher betrachteten sogen. gemeinen Z. unterscheidet man noch Epizykloiden und Hypozykloiden; sie werden von einem Punkte des Kreisumfanges beschrieben, wenn der Kreis statt auf einer Geraden auf einem festen Kreise hinrollt, und zwar die eine oder die andre, je nachdem der bewegliche Kreis auf der äußern oder auf der innern Seite des festen Kreises hinrollt.
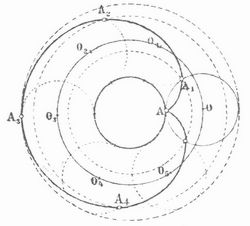
In Fig. 2 ist eine Epizykloide dargestellt, bei welcher der feste und der bewegliche Kreis gleich groß sind; O, O1, O2,... sind die verschiedenen Lagen des Mittelpunktes des letztern, A, A1, A2,... die entsprechenden Lagen des Punktes A, der die Kurve beschreibt.
http://www.zeno.org/Meyers-1905. 1905–1909.