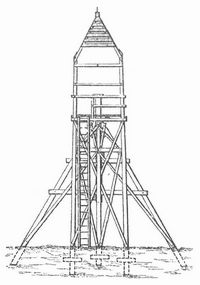
Signale, trigonometrische
Schlagen Sie auch in anderen Wörterbüchern nach:
Trigonometrische Netzlegung — Trigonometrische Netzlegung, s. Triangulation. T. Reihen, soviel wie Fouriersche Reihen. T. Signale, s. Signale, trigonometrische … Meyers Großes Konversations-Lexikon
Trigonometrische Vermessungen, T. Signale, T-s Netz — Trigonometrische Vermessungen, T. Signale, T s Netz, s.u. Aufnehmen … Pierer's Universal-Lexikon
Triangulierung [1] — Triangulierung (Triangulation, Dreiecksmessung, trigonometrische Punktbestimmung), geodätische Bestimmungsmethode. Sie bestimmt für ein System von Festpunkten (Dreieckspunkten, trigonometrischen Punkten oder Stationen), das im Gelände dauerhaft… … Lexikon der gesamten Technik
Fourier-Analysis — Die Fourier Analysis (Aussprache des Namens: fur je) auch bekannt als Fourier Analyse oder klassische harmonische Analyse ist die Theorie der Fourier Reihen und Fourier Integrale. Ihre Ursprünge reichen in das 18. Jahrhundert zurück. Benannt sind … Deutsch Wikipedia
Fourierreihe — Als Fourierreihe (nach Jean Baptiste Joseph Fourier) einer periodischen Funktion f, die abschnittsweise stetig ist, bezeichnet man deren Entwicklung in eine Funktionenreihe aus Sinus und Kosinusfunktionen. Die Basisfunktionen der Fourierreihe… … Deutsch Wikipedia
Kosinus — Graphen der Sinus und der Cosinusfunktion Die Sinusfunktion und die Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen aus der Klasse der trigonometrischen Funktionen. Sinus und Kosinus sind grundlegend in allen… … Deutsch Wikipedia
Kosinus und Sinus — Graphen der Sinus und der Cosinusfunktion Die Sinusfunktion und die Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen aus der Klasse der trigonometrischen Funktionen. Sinus und Kosinus sind grundlegend in allen… … Deutsch Wikipedia
Sinus — Graphen der Sinus und der Cosinusfunktion Die Sinusfunktion und die Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen aus der Klasse der trigonometrischen Funktionen. Sinus und Kosinus sind grundlegend in allen… … Deutsch Wikipedia
Sinusfunktion — Graphen der Sinus und der Cosinusfunktion Die Sinusfunktion und die Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen aus der Klasse der trigonometrischen Funktionen. Sinus und Kosinus sind grundlegend in allen… … Deutsch Wikipedia
Sinusschwingung — Graphen der Sinus und der Cosinusfunktion Die Sinusfunktion und die Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen aus der Klasse der trigonometrischen Funktionen. Sinus und Kosinus sind grundlegend in allen… … Deutsch Wikipedia