Parallelenaxiom

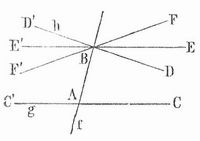
Parallelenaxiom, die fünfte Forderung, deren Euklid zum Aufbau der Geometrie bedarf, sehr oft fälschlich als sein elftes Axiom bezeichnet. Es läßt sich so ausdrücken: werden zwei gerade Linien g und h (Fig. 1) einer Ebene von einer dritten Geraden f so geschnitten, daß auf der einen Seite von t die beiden entstehenden innern Winkel (hier die Winkel CAB und ABD) zusammen weniger als zwei Rechte betragen, so schneiden g und h, genügend verlängert, einander auf eben dieser Seite von k; g und h schneiden einander also, wenn man g über C hinaus und h über D hinaus verlängert, während sie auf der andern Seite von f, wo die Summe der innern Winkel C´AB u. ABD´ größer als zwei Rechte ist, umso weiter auseinander gehen, je mehr man g über C´ u. h über D´ hinaus verlängert.

Fig. 1.

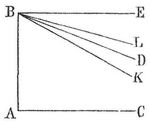
Denkt man sich durch B eine Gerade BE derart gezogen, daß die Summe der innern Winkel CAB und ABE gerade gleich zwei Rechten ist, so läßt sich auf Grund der vorhergehenden Axiome Euklids beweisen, daß die Gerade BE, wie weit man sie auch über E hinaus oder nach der andern Seite, über E´ hinaus, verlängern mag, niemals mit g zusammentrifft, daß sie also nach der Erklärung des Begriffs parallel (s. d.) zu g parallel ist. Das Euklidische P. hat daher zur Folge, daß jede Gerade BD, die man im Innern des Winkelraums ABE ziehen kann, genügend weit verlängert die Verlängerung der Geraden g oder AC trifft, wie klein auch der Winkel EBD sein mag, und daß ebenso jede Gerade BF´, die man im Innern des Winkelraums ABE´ ziehen kann, über F´ hinaus verlängert die Verlängerung von g über C´ hinaus treffen muß (weil nämlich hier die Summe der innern Winkel C´AB und ABE´ gleich zwei Rechten, also die Summe der Winkel C´AB und ABF´ kleiner als zwei Rechte ist). Kurz, das P. kommt darauf hinaus, daß die Gerade E´BE die einzige zu g parallele Gerade ist, die man durch den Punkt B ziehen kann. Auf Grund des P. läßt sich ferner beweisen, daß die Winkelsumme in jedem geradlinigen Dreieck gleich zwei Rechten ist, daß alle Lote, die man von den Punkten einer Geraden auf eine zweite, zu ihr parallele Gerade fällen kann, gleich lang sind, etc., lauter Sätze, die innerhalb der uns zugänglichen Räume durch die Erfahrung bestätigt werden, und die uns infolge langer Gewöhnung viel einleuchtender erscheinen als das Euklidische P. Infolgedessen hat man von jeher versucht, das P. als überflüssig nachzuweisen, d.h. zu zeigen, daß es eine Folge der andern Axiome Euklids ist, oder doch, weil das nicht gelingen wollte, es durch ein einleuchtenderes Axiom zu ersetzen. Diese Versuche sind bis auf die neueste Zeit immer wiederholt worden und werden es auch noch heutzutage, obwohl sich inzwischen herausgestellt hat, daß sie vergeblich sein müssen. Dieser Erkenntnis waren Saccheri (1733) und Lambert (1766), die äußerst schöne Untersuchungen über das P. angestellt haben, schon sehr nahe; Gauß erfaßte sie als erster mit voller Klarheit, freilich ohne etwas darüber zu veröffentlichen. Der Welt bekannt geworden ist sie durch Lobatschefskij und J. Bolyai, die Begründer der nichteuklidischen Geometrie. Diese Geometrie verzichtet auf das Euklidische P. vollständig, sie läßt daher die Möglichkeit offen, daß sich auch innerhalb des Winkelraums ABE noch eine Gerade, z. B. BD, ziehen läßt, die mit AC niemals zusammentrifft, wie weit man auch beide Gerade über D und C hinaus verlängern mag. In diesem Falle wird auch jede Gerade, die man innerhalb des Winkelraums DBE durch B ziehen kann, die Verlängerung von AC niemals treffen, es gibt also dann nach der Euklidischen Erklärung des Wortes parallel unendlich viele Gerade durch B, die zu g parallel sind. Nimmt man der Einfachheit wegen jetzt an, daß die Winkel CAB und ABE, die zusammen zwei Rechte betragen, beide rechte Winkel sind (Fig. 2), so wird es in dem Winkelraum ABE eine Gerade BD geben von der Art, daß sie selbst die Gerade AC niemals trifft, wie weit man auch über D und C hinaus verlängern mag, während jede Gerade BK im Innern des Winkelraums ABD genügend weit verlängert AC schließlich trifft, wie klein auch der Winkel KBD sein mag. Diese Gerade trennt dann innerhalb des Winkelraums ABE die durch B gehenden Geraden, die AC schneiden, von denen, die AC nicht schneiden, denn jede Gerade BL innerhalb des Winkelraums DBE wird AC niemals treffen, wie weit man sie auch über L hinaus verlängern mag.

Fig. 2.

In der nichteuklidischen Geometrie bezeichnet man die eben beschriebene Gerade BD als die durch B gehende Parallele zu AC, und den spitzen Winkel ABD nennt man den zu dem Lote AB gehörigen Parallelwinkel, die im Winkelraum DBE liegenden Geraden wie BL nennt man nichtschneidende Gerade. In dieser Weise kann man nun eine vollständige, widerspruchsfreie Geometrie aufbauen, eben die nichteuklidische Geometrie. Es ergibt sich, daß die Winkelsumme im geradlinigen Dreieck kleiner ist als zwei Rechte und um so kleiner, je größer der Inhalt des Dreiecks ist, daß zwei Dreiecke wit gleichen Winkeln stets auch kongruent sind, daß also ähnliche Dreiecke nicht existieren etc. Hierdurch ist einerseits bewiesen, daß das Euklidische P. eine wirklich neue Annahme ist, die aus den frühern Axiomen nicht folgt, anderseits aber, daß Euklid bei der Fassung seines Axioms gerade den Punkt getroffen hat, auf den es ankommt; denn kein Axiom, durch das man das Euklidische P. hat ersetzen wollen, ist so geeignet wie dieses, wenn man die Möglichkeit des Gegenteils untersuchen will, also die Möglichkeit, daß es nicht erfüllt ist. Man vergleiche nur das Axiom von John Wallis (1663): »Zu jedem Dreieck läßt sich ein ähnliches in beliebigem Maßstabe zeichnen«, oder das von Legendre: »Durch jeden Punkt innerhalb der Öffnung eines Winkels läßt sich eine Gerade ziehen, die beide Schenkel des Winkels trifft«, oder das von W. Bolyai: »Drei Punkte, die nicht in gerader Linie liegen, liegen stets auf einem Kreise«. So interessant nun auch diese Untersuchungen sind, bei denen man das Euklidische P. fallen läßt, so wird dieses doch immer seinen Platz behaupten als die Annahme, die innerhalb der Grenzen unsrer Erfahrung mit der Wirklichkeit in so hohem Grad übereinstimmt, daß wir keine Abweichung davon bemerken können, die also für alle Anwendungen der Geometrie in Mechanik, Physik, ja selbst Astronomie ganz allein in Betracht kommt. Über die Geschichte des Parallelenaxioms vgl. Stäckel und Engel, Die Theorie der Parallellinien von Euklid bis auf Gauß (Leipz. 1895). S. auch Geometrie.