Parallele Kräfte

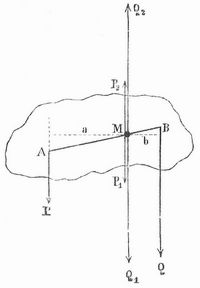
Parallele Kräfte. Um die Wirkung zweier paralleler und gleichgerichteter Kräfte (P und Q der Fig. 1), die an zwei fest miteinander verbundenen Punkten (A und B) eines starren Körpers angreifen, zu ermitteln, denken wir uns an einem Punkt (M), der auf der Verbindungslinie (AB) der beiden Angriffspunkte liegt, zwei Kräfte (P₁ und Q₁) parallel, gleich und gleichgerichtet den gegebenen Kräften (P und Q), und noch zwei Kräfte (P₂ und Q₂), die den gegebenen ebenfalls parallel und gleich, aber entgegengesetzt gerichtet sind, angebracht.

Parallele Kräfte.

Da die Kraft P, von der gleichen, aber entgegengesetzt wirkenden P₂ aufgehoben und ebenso die Kraft Q₁ durch die Kraft Q₂ vernichtet wird, so ist dadurch an dem Zustande des Körpers nicht das mindeste geändert. Die Kraft P bildet aber mit der Kraft P₂ ein Kräftepaar (s. d.), das den Körper um eine zur Ebene, in der die Kräfte P und Q liegen (d.h. zur Ebene der Zeichnung), senkrechte Achse zu drehen strebt, während die Kraft Q mit der Kraft Q₂ ebenfalls ein Kräftepaar bildet, das den Körper in der entgegengesetzten Richtung zu drehen bestrebt ist. Wählen wir nun die Lage des Punktes M so, daß diese beiden entgegengesetzten Drehungsbestrebungen einander gleich werden, so heben sie sich auf, und es bleiben von sämtlichen Kräften nur noch die am Punkt M wirkenden Kräfte P, und Q, übrig, die, da sie nach derselben Richtung wirken, durch eine einzige Kraft, die gleich ihrer Summe, also gleich der Summe der gegebenen Kräfte P und Q ist, ersetzt werden können. Damit aber die Drehungsbestrebungen (Momente) der beiden Kräftepaare einander gleich werden, so muß man den Punkt M so wählen, daß der Arm des Kräftepaares PP₂, d.h. die von M auf die Richtung der Kraft P gezogene Senkrechte (a), mit der Kraft P multipliziert dasselbe Produkt gebe wie der Arm (b) des Kräftepaares QQ₂ multipliziert mit der Kraft Q, d.h. der Punkt M muß so liegen, daß die Arme a und b und demnach auch die Strecken MA und MB sich umgekehrt verhalten wie die zugehörigen Kräfte (nämlich wie Q zu P). Es ergibt sich also, daß zwei parallele gleichgerichtete Kräfte (Seitenkräfte oder Komponenten) durch eine einzige Kraft (Mittelkraft oder Resultante) ersetzt werden können, die gleich ihrer Summe ist und an einem Punkt angreift, der die Strecke zwischen den beiden Angriffspunkten im umgekehrten Verhältnis der beiden Kräfte teilt. Durch wiederholte Anwendung dieses Satzes lassen sich beliebig viele p. K. von gleicher Richtung zu einer einzigen Mittelkraft zusammenfassen, indem man die Mittelkraft der beiden ersten Kräfte mit der dritten, die neue Mittelkraft mit der vierten Kraft etc. vereinigt; man findet so schließlich eine Gesamtmittelkraft, die gleich der Summe aller gegebenen Kräfte ist und an einem bestimmten Punkt angreift, den man den Mittelpunkt (das Zentrum) der parallelen Kräfte nennt. Jener Satz lehrt ferner, eine gegebene Kraft, die man als Mittelkraft betrachtet, in zwei zu ihr parallele Seitenkräfte, die zusammengenommen ihr gleich sind, zu zerlegen. Soll eine an einer wagerechten Stange hängende Last von zwei verschieden kräftigen Menschen, z. B. einem Knaben und einem Mann, getragen werden, so wird man die Last um so weiter von dem Knaben weg aufhängen, je kräftiger der Mann im Verhältnis zum Knaben ist, weil sich die Last im umgekehrten Verhältnis ihrer Entfernungen von den Stangenendpunkten auf diese verteilt.

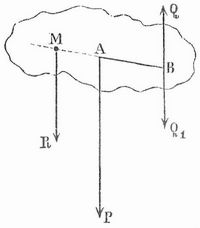
Greifen an zwei Punkten (A und B, Fig. 2) eines Körpers zwei parallele ungleiche und entgegengesetzt gerichtete Kräfte an, so kann man die größere derselben (P) in zwei Seitenkräfte zerlegen, deren eine Q, der Kraft Q gleich und entgegengesetzt mit ihr an demselben Punkt B wirkt, und deren andre (R), gleich dem Unterschied von P und Q, an einem Punkt M angreift, der auf der über A hinaus verlängerten Verbindungslinie der Angriffspunkte A und B so liegt, daß sich MA zu AB verhält wie Q zu dem Unterschied von P und Q oder, was dasselbe ist, MA zu MB wie Q zu P.

Fig. 2. Parallele Kräfte.

Da die Kräfte Q und Q₁ sich gegenseitig aufheben, so bleibt als Mittelkraft, welche die beiden Kräfte vollkommen ersetzt, nur noch die Kraft R übrig, die gleich dem Unterschiede der gegebenen Kräfte ist und an einem Punkte der Geraden AB angreift, dessen Entfernungen von den Angriffspunkten A und B sich umgekehrt verhalten wie die zugehörigen Kräfte. Sind die beiden parallelen und entgegengesetzt wirkenden Kräfte einander gleich, so ist dieses Verfahren nicht durchführbar; die beiden Kräfte bilden alsdann ein Kräftepaar (s. d.) und besitzen keine Mittelkraft.