Orographie

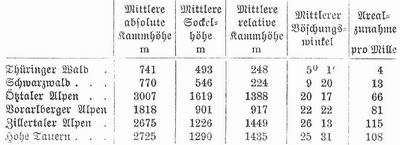
Orographie (griech.), Beschreibung der Gebirge nach ihren äußern Formen und Gruppierungen, in weiterer, jetzt üblicher Auffassung die Lehre von den Reliefformen der Erdoberfläche überhaupt sowie von ihrer Entstehung und ihrer allmählichen Umbildung und Veränderung (allgemeine O. oder Morphologie der Erdoberfläche). Die O. im weitern Sinne hat also nicht nur in der sogen. Oroplastik oder Morphographie (d.h. Gestaltlehre) die große Mannigfaltigkeit der Formen der Erdoberfläche zu schildern, sondern auch in der Orometrie oder Morphometrie die Formen auszumessen und zur Darstellung zu bringen sowie die rechnerischen Methoden auseinanderzusetzen, mit deren Hilfe dieses möglich wird, und endlich in der Orogenie die Ursachen und die Kräfte, denen die Formen der Erdoberfläche ihre Entstehung und fortdauernde Veränderung und Umbildung verdanken, zu untersuchen. Die O., zusammen mit der Hydrographie (s. d.), die gleichsam nur eine Unterabteilung der allgemeinen O. darstellt, bildet einen Teil der physikalischen Geographie; ihre wichtigsten Hilfswissenschaften sind Geodäsie und Geologie. Erstere findet besonders Anwendung in der Orometrie und zumal in der Kartographie oder Herstellung orographischer Karten (Landkarten, s. d.), die, seit etwa 50 Jahren in hoher Vollendung ausgeführt, nicht bloß die Gebirgszüge und Flußläufe, sondern alle Formen der Erdoberfläche überhaupt in großer Klarheit wiederzugeben imstande sind, entweder durch Anwendung von Farbentönen, oder durch Bergschraffur, oder durch Höhenkurven oder Isohypsen (Horizontalen in gleichen Vertikalabständen) oder durch eine Kombination derartiger Angaben. Die Orometrie speziell bestimmt das Verhältnis von Wasser und Land, die Gliederung der Wasser- und Landflächen, den vertikalen Aufbau der Erdkruste, das Areal und Volumen der Gebirge (s. d.), ihre Gipfel-, Paß- und Kammhöhen, die mittlere Gipfelhöhe und mittlere Paßhöhe sowie (die Differenz zwischen diesen beiden, d.h. die mittlere Schartung) ferner die mittlere Böschung sowie das von dieser abhängige Verhältnis der Gesamtoberfläche zu dem Areal der Basis (die sogen. Arealszunahme der Oberfläche), die Länge, die mittlere Höhe und das durchschnittliche Gefälle der Täler, dann die mittlere Sockelhöhe (d.h. der Durchschnitt aus den mittlern Höhen aller Täler) und (die Differenz zwischen dieser und der mittlern absoluten Kammhöhe, d.h. die relative mittlere Kammhöhe) ferner die Verteilung der Erhebungen etc. Sie vergleicht die nach bestimmten Methoden ermittelten Werte miteinander, indem sie dieselben in ähnlicher Weise, wie es die nachfolgende, von Neumann gegebene Tabelle veranschaulicht, zusammenstellt, und vervollkommt die Rechnungsmethoden, die zur Auffindung jener und ähnlicher Werte führen.

Die Orogenie betrachtet ebenso wie die Geologie (s. d.) die auf der festen Erdkruste wirksamen Naturkräfte in ihren gestaltenden Wirkungen, aber weit weniger als jene bezüglich der sich bildenden Ablagerungen als vielmehr in Rücksicht auf die dabei entstehenden Formen. Als der eigentliche Begründer der O. gilt Bernhard Varenius (»Geographia generalis«, Amsterd. 1650). Gefördert wurde sie namentlich durch Playfair (»Illustrations of the Huttonian theory«. 1802) und Karl Friedrich Struve (»Physiognomik der Erde«, Leipz. 1802), durch Karl Ritter (»Die Erdkunde«, Berl. 1817), A. v. Humboldt und in neuerer Zeit besonders durch v. Sonklar (»Allgemeine O.«, Wien 1873), v. Richthofen (»Führer für Forschungsreisende«, Berl. 1886; Neudruck Hannover 1901), A. Penck (»Morphologie der Erdoberfläche«, Stuttg. 1894), de la Noë und de Margerie (»Les formes du terrain«, Par. 1888) und J. Geikie (»Earth sculpture or the origin of land-forms«, Lond. 1898). Wichtige orometrische Untersuchungen stellten in neuerer Zeit hauptsächlich Krümmel und Penck, auch Peucker und L. Neumann (»Orometrie des Schwarzwalds«, Wien 1886; »Orometrische Studien« in der »Zeitschrift für wissenschaftliche Geographie«, 1888, etc.) an. Vgl. Kändler, Kritik orometrischer Werte (Leipz. 1899), und Supan, Grundzüge der physischen Erdkunde (3. Aufl., das. 1903).