Prisma

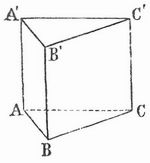
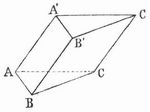
Prisma (griech., »das Abgesägte«), ein zur Klasse der Polyeder gehöriger Körper, der erhalten wird, wenn man in zwei parallelen Ebenen zwei einander kongruente geradlinige Polygone so wählt, daß die Seiten des einen den entsprechenden Seiten des andern parallel sind, und dann die Ecken des einen Polygons mit den entsprechenden des andern durch gerade Linien (die Kanten des Prismas) verbindet. Das P. wird dann begrenzt durch jene beiden Polygone (die Grund- und die Deckfläche) und durch die Parallelogramme, die je zwei entsprechende Seiten der Polygone mit den Verbindungslinien ihrer Endpunkte bilden. Solcher Parallelogramme (Seitenflächen des Prismas) gibt es so viele, wie die Grundfläche Seiten hat, man spricht daher von drei-, vier- und vielseitigen Prismen. Ein dreiseitiges P. erhält man mithin, wenn man in zwei parallelen Ebenen zwei kongruente Dreiecke A, B, C und A', B', C' so annimmt, daß die Seiten AB, BC, CA des einen der Reihe nach den Seiten A'B', B'C', C'A' des andern parallel sind, und dann die Geraden (Kanten) AA', BB', CC' zieht; die Seitenflächen des Prismas sind dann die drei Parallelogramme ABB'A', BCC'B' und CAA'C' (Fig. 1 u. 2). Ein vierseitiges P., dessen Grundfläche ein Parallelogramm ist, nennt man auch Parallelepipedon.

Fig. 1. Gerades dreiseitiges Prisma.

Fig. 2. Schiefes dreiseitiges Prisma.

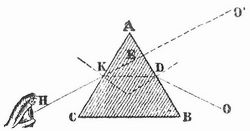
Jedes vielseitige P. kann man durch Diagonalschnitte, d. h. durch Ebenen, die je zwei nicht derselben Seitenfläche des Prismas angehörige Kanten enthalten, in lauter dreiseitige Prismen zerlegen. Man unterscheidet ferner gerade oder normale Prismen, bei denen die Kanten senkrecht auf den Grundflächen stehen, und schiefe. Fig. 1 zeigt ein gerades, Fig. 2 ein schiefes P. Der senkrechte Abstand zwischen den beiden Grundflächen heißt die Höhe des Prismas, beim geraden P. ist diese gleich der Länge einer Kante des Prismas. Der Rauminhalt des Prismas ist gleich dem Produkt aus Grundfläche und Höhe. Schneidet man von einem P. durch eine zur Grundfläche nicht parallele Ebene ein Stück ab, so erhält man ein schief abgeschnittenes P. Denkt man sich als Grundfläche des Prismas ein Polygon mit unendlich vielen, unendlich kleinen Seiten oder, was auf dasselbe hinauskommt, eine geschlossene krumme Linie, so verwandelt sich das P. in einen Zylinder. – In der Kristallographie heißen Prismen vier- oder achtflächige, drei-, sechs- oder zwölfflächige Kristallformen, die nur seitlich, nicht aber oben und unten von Flächen begrenzt werden und deshalb im Gegensatz zu den geschlossenen Formen als offene bezeichnet werden (vgl. Kristall). Prismen, denen nach der kristallographischen Ableitung eine liegende Stellung zukommt, werden als Domen (s. Doma) bezeichnet. – In der Physik heißt P. ein durchsichtiger Körper mit zwei keilförmig zueinander geneigten glatten Flächen, durch die das Licht ein- und austreten kann. Die gewöhnlich gebrauchten Glasprismen haben die Gestalt einer dreiseitigen Säule, deren Querschnitt (Hauptschnitt) ein gleichseitiges Dreieck ABC ist (Fig. 3); nur zwei Seitenflächen des Prismas (BA und CA) brauchen poliert zu sein, die dritte Seitenfläche BC, die dem »brechenden Winkel« A gegenüberliegt, sowie die beiden dreieckigen Endflächen werden zweckmäßig matt geschliffen und geschwärzt.

Fig. 3. Prisma.

Ein Lichtstrahl, der in der Richtung OD auf die eine Seitenfläche trifft, schlägt den Weg ODKH ein, indem er durch die sowohl beim Eintritt als beim Austritt stattfindende Brechung abgelenkt wird. Der Strahl wird, wie die Zeichnung lehrt, von der Kante weg nach dem dicken Teil des Keiles abgelenkt; ein Auge, das von H aus durch das P. blickt, sieht daher die hinter dem P. befindlichen Gegenstände nach der Kante hin verschoben, z. B. den Punkt O nach O'. Der Winkel OEO', den die Richtung des eintretenden Strahles OD mit der Richtung KH des austretenden Strahles bildet, gibt die gesamte Ablenkung an, die der Strahl durch die zweimalige Brechung erlitten hat. Diese Ablenkung fällt am kleinsten aus (Minimum der Ablenkung), wenn der durchgehende Strahl mit den beiden brechenden Flächen gleiche Winkel bildet. Mißt man den brechenden Winkel A eines Prismas und die kleinste Ablenkung, die es hervorbringt, so kann man daraus mit Rücksicht auf das Brechungsgesetz (s. Brechung des Lichtes) das Brechungsverhältnis des Stoffes, aus dem das P. verfertigt ist, leicht berechnen. Bezeichnet nämlich β den brechenden Winkel BAC des Prismas, α die kleinste Ablenkung OEO', so ist das Brechungsverhältnis n = sin.¹/₂(α + β):sin.¹/₂β. Man gibt daher den Körpern, deren Brechungsverhältnis man durch dieses sehr genaue Verfahren bestimmen will, die Gestalt eines Prismas, was bei Flüssigkeiten dadurch geschieht, daß man sie in ein Hohlprisma füllt, dessen brechende Flächen durch ebene Glasplatten mit parallelen Flächen gebildet werden. Die Messungen der Ablenkung sowohl als des brechenden Winkels werden vorgenommen mittels des Spektrometers oder des Goniometers. (Über Dispersion durch das P. s. Dispersion; Reflexionsprisma, s. Brechung; achromatisches P., s. Achromatismus; geradsichtiges [anapoklitisches] P., s. Spektralanalyse.) Prismensysteme, d. h. Zusammenstellungen mehrerer Prismen, werden gebraucht, um sehr starke Dispersion zu erzielen. Das Trennungs- (Auflösungs-)Vermögen eines solchen hängt nicht allein von der Winkeldifferenz ab, die durch die Dispersion den verschiedenfarbigen Bildern des Spaltes erteilt wird, sondern auch von der Breite der Strahlenbündel, welche die Abbildung des Spaltes vermitteln.