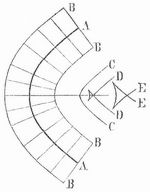
Parallelkurven

Parallelkurven

Parallelkurven und Parallelflächen. Errichtet man in jedem Punkt einer ebenen Kurve (einer Fläche) auf der zu dem Punkte gehörigen Tangente (Tangentialebene) ein Lot von fester Länge und zwar immer nach derselben Seite der Kurve (Fläche) hin, so bilden die Endpunkte aller dieser gleichlangen Lote eine Parallelkurve (Parallelfläche) zu der gegebenen Kurve (Fläche).

Parabel mit Normalen und Parallelkurven.
Parabel mit Normalen und Parallelkurven.

Jedem Punkte der gegebenen Kurve (Fläche) entspricht so ein Punkt der Parallelkurve (Parallelfläche), und die zu entsprechenden Punkten beider Kurven (Flächen) gehörigen Tangenten (Tangentialebenen) sind einander parallel, daher der Name. Führt man die Konstruktion für jede beliebige Länge der Lote und auf beiden Seiten der gegebenen Kurve (Fläche) aus, so erhält man alle Parallelkurven (Parallelflächen) zu der gegebenen; z. B. sind die Parallelkurven zu einer Geraden: alle ihr parallelen Geraden, zu einem Kreis: alle Kreise mit demselben Mittelpunkt. Ebenso sind die Parallelflächen zu einer Ebene: alle ihr parallelen Ebenen, zu einer Kugel: alle Kugeln mit demselben Mittelpunkt. In der Figur sind BB, CC, DD, EE lauter Parallelkurven zu der Parabel AA. Der Begriff der Parallelfläche spielt in der von Huygens begründeten Undulationstheorie des Lichtes eine Rolle.


http://www.zeno.org/Meyers-1905. 1905–1909.

Игры ⚽ Нужно решить контрольную?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Parallelkurven — einer gegebenen Kurve entstehen, wenn man auf jeder Normale derselben nach beiden Seiten eine konstante Strecke abträgt. Die beiden hierdurch entstehenden Kurvenzüge sind im allgemeinen Teile einer Kurve. Die Parallelkurve ist auch Enveloppe… …   Lexikon der gesamten Technik

  • Erwin Voellmy — (* 9. September 1886 in Herzogenbuchsee; † 15. Januar 1951 in Basel) war ein Schweizer Schachmeister. Inhaltsverzeichnis 1 Leben 2 Schriften 3 Literatur …   Deutsch Wikipedia

  • Voellmy — Erwin Voellmy (* 9. September 1886 in Herzogenbuchsee; † 15. Januar 1951 in Basel) war ein schweizerischer Schachmeister. Inhaltsverzeichnis 1 Leben 2 Schriften 3 Literatur 4 Weblinks …   Deutsch Wikipedia

  • Parallelflächen — Parallelflächen, s. Parallelkurven …   Meyers Großes Konversations-Lexikon

  • Enveloppen — Enveloppen. a) In der ebenen analytischen Geometrie ist eine Enveloppe (Hüllkurve, einhüllende Kurve) der Ort der Schnittpunkte benachbarter Kurven einer Kurvenschar. Dieselbe berührt alle Kurven der Schar. Ist f (x, y; z; λ) = 0 die… …   Lexikon der gesamten Technik

  • Evolvente — einer Kurve (Grundkurve) wird beschrieben von einem Punkte einer Tangente der Grundkurve, wenn erstere auf letztere ohne zu gleiten rollt. Die unendlich vielen Evolventen einer Kurve sind gegenseitige Parallelkurven. Die Differentialgleichung der …   Lexikon der gesamten Technik

  • Kurven — Kurven, krumme Linien, stetige Reihen von Punkten in der Ebene. Eine solche wird durch eine Gleichung zwischen zwei Veränderlichen f (x, y) = 0 oder homogen f (x, y, ω) = 0, aufgelöst y = φ (x) dargestellt. Je nach der Natur der… …   Lexikon der gesamten Technik

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”