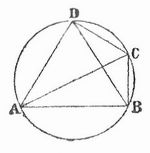
Kreisviereck — Kreisviereck, Viereck, um welches sich ein Kreis beschreiben läßt, d.h. welches sich so in einen Kreis legen läßt, daß seine vier Ecken Punkte auf dem Umfange jenes sind. Jedes Viereck ist ein K., wenn einer der vier folgenden Sätze von ihm gilt … Pierer's Universal-Lexikon
Kreisviereck — Ein Sehnenviereck ABCD mit Umkreis k Ein Sehnenviereck ist ein Viereck, dessen Eckpunkte auf einem Kreis liegen, dem Umkreis des Vierecks. Folglich sind alle Seiten des Sehnenvierecks Sehnen des Umkreises. Üblicherweise meint man mit… … Deutsch Wikipedia
Diagonāle — (v. gr., Diagonallinie), jede durch die Winkelspitzen einer geradlinigen ebenen Figur od. eines ebenflächigen Körpers gezogene Gerade, ohne eine Kante von diesem od. eine Seite von jener zu sein. Im Dreieck gibt es demnach keine D., wohl aber im… … Pierer's Universal-Lexikon
Kreis — Kreis, 1) (Circulus, Math.), eine ebene geschlossene Linie, deren Punkte alle von einem gewissen Punkte gleiche Entfernung haben. Dieser Punkt heißt Mittelpunkt (Centrum); die vom Kreise begrenzte Fläche heißt Kreisfläche u. der K. selbst zum… … Pierer's Universal-Lexikon
Ptolemäischer Satz — Ptolemäischer Satz, s. Kreisviereck … Meyers Großes Konversations-Lexikon
Viereck — (Tetragon), in der Geometrie jede von vier geraden Linien, den Seiten, eingeschlossene Figur mit vier Ecken. Liegen alle vier Seiten in einer Ebene, so ist das V. eben, sonst windschief. In jedem ebenen V. ist die Winkelsumme gleich 360°. Sind je … Meyers Großes Konversations-Lexikon
Sehnenviereck — Sehnenvier|eck, Kreisviereck, Geometrie: Viereck, dessen Seiten Sehnen eines Kreises sind. Im Sehnenviereck ist die Summe der Größen zweier gegenüberliegender Winkel stets gleich 180 º. (ptolemäischer Satz) … Universal-Lexikon