- Bodendruck einer Flüssigkeit
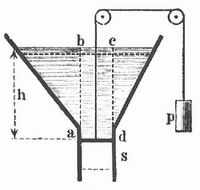
Bodendruck einer Flüssigkeit, der Druck, den eine Flüssigkeit auf den Boden des Gefäßes, in dem sie sich befindet, ausübt. Der Boden eines Gefäßes sei dicht schließend in einer vertikalen Ansatzröhre beweglich (s. Abbild.) und durch eine entsprechend (mit dem Gewicht p) belastete, über Rollen geführte Schnur gehalten.
Schiebt man den Boden um die Strecke s abwärts, so steigt p ebensoviel in die Höhe, somit wird die potentielle Energie p.s gewonnen. Gleichzeitig kommt unten die Flüssigkeitsmenge q.s hinzu (wenn q die gedrückte Fläche bedeutet), während oben (in der Höhe h) eine gleichgroße Flüssigkeitsmenge verschwindet. Dies bedingt einen Verlust an potentieller Energie = q.s.d.h, wenn d das spezifische Gewicht der Flüssigkeit ist. Nach dem Gesetz der Erhaltung der Energie müssen Gewinn und Verlust sich decken, somit muß sein: p.s = q.s.d.h oder p = q.d.h., d. h. der gesuchte Druck ist gleich dem Gewichte der über der gedrückten Fläche stehenden vertikalen Flüssigkeitssäule a b c d, gleichgültig, welches die Form des Gefäßes ist. In einem Gefäß, das sich nach oben erweitert, ist hiernach der auf den Boden ausgeübte Druck kleiner, in einem nach oben enger werdenden Gefäß z. B. in einer Flasche) größer als das Gewicht der im Gefäß enthaltenen Flüssigkeit (hydrostatisches Paradoxon). In der Realschen Presse (s. Auslaugen) findet dieses Verhalten praktische Verwertung. Für ein kleines Flächenelement behält der Satz auch seine Gültigkeit, wenn dasselbe nicht vertikal abwärts, sondern z. B. seitlich in horizontaler Richtung verschiebbar ist. Der Druck auf eine ausgedehnte Seitenwand ist gleich der Summe der Drucke auf ihre einzelnen Elemente.
http://www.zeno.org/Meyers-1905. 1905–1909.