Zentralbewegung

Zentralbewegung, Bewegung eines Körpers, der, nachdem ihm eine Anfangsgeschwindigkeit erteilt worden, der Einwirkung einer Kraft überlassen wird, die stets nach einem festen Mittelpunkt (Zentrum) hin gerichtet ist.

Zentralbewegung.

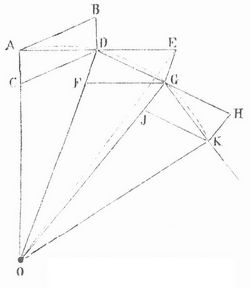
Der Körper, der vermöge seiner Trägheit in der Richtung A B (s. Figur) mit der ihm innewohnenden Geschwindigkeit in gleichförmiger Bewegung fortzugehen strebt, wird durch die nach dem Mittelpunkt O wirkende Zentral- oder Zentripetalkraft von der Linie A B abgezogen; ist A C die Strecke, um die diese Kraft ihn dem Zentrum nähert in der Zeit, während der er vermöge der Trägheit von A nach B gelangen würde, so findet man den Ort I), den er nach dieser Zeit tatsächlich einnimmt, als Durchschnittspunkt der Linien C D und B D, die beziehungsweise parallel mit A B und A C gezogen werden (s. Parallelogramm der Kräfte). Der Weg, den der Körper von A bis D zurücklegt, ist eigentlich bogenförmig gekrümmt, fällt aber um so genauer mit der geraden Verbindungslinie A D zusammen, während eines je kleinern Zeitraums man die Bewegung betrachtet. Nimmt man daher diesen Zeitraum hinlänglich klein an, so darf der Weg von A bis D als geradlinig angesehen werden. Während eines zweiten gleichgroßen Zeitteilchens würde der Körper vermöge seiner Trägheit unter Beibehaltung seiner in D vorhandenen Richtung und Geschwindigkeit die Strecke 1) E zurücklegen, die gleich A D ist, wenn er nicht durch die von D nach O hin wirkende Zentralkraft von der Linie D E um die Strecke D F abgezogen und nach dem Eckpunkt G des Parallelogramms D E G F zu gehen genötigt würde, die er auf dem Wege D G erreicht. Ebenso wird er während des dritten gleichgroßen Zeitteilchens, statt die mit D G gleiche und gleichgerichtete Strecke G H infolge seiner Trägheit zu durchlaufen, nach dem Eckpunkt K des Paralellogramms G H K J gelangen etc. Der Körper durchläuft also unter dem Einfluß der ihn unausgesetzt nach dem Zentrum O hinziehenden Zentral kraft die krummlinige Bahn A D G K, der die gebrochene Linie A D G K um so näher kommt, je kleiner die der Betrachtung zugrunde gelegten, Zeitteilchen angenommen werden. Die Bewegungsrichtung, die der Körper in jedem Punkte seiner gekrümmten Bahn besitzt, wird angegeben durch die in diesem Punkt an die Bahn gelegte Berührungslinie (Tangente). Die geradlinige Bewegung, die der Körper längs dieser Tangente infolge seines Beharrungsvermögens annehmen würde, wenn in irgendeinem Augenblick die Zentralkraft aufhörte zu wirken, nennt man deswegen seine Tangentialbewegung. Die vom Mittelpunkt O nach dem bewegten Körper gezogen gedachte gerade Linie, nach der die Kraft wirkt, heißt der Leitstrahl oder Radius vector des Körpers. Während der Körper von A nach D übergeht, durchstreicht sein Leitstrahl den Flächenraum A O D, beim Übergang von D nach C den Flächenraum D O G etc. Diese Flächenräume, die eigentlich von den krummlinigen Bahnstücken A D, D G etc. begrenzt sind, unterscheiden sich von den Dreiecken A O D, D O G etc. um so weniger, je kleiner die zugehörigen gleichen Zeitteilchen sind. Man erkennt nun leicht, daß die Dreiecke A O D und D O G, weil sie beide dem Dreieck D O E an Flächeninhalt gleich sind, auch unter sich flächengleich sind, und so überhaupt jedes folgende Dreieck mit dem vorhergehenden. Es ergibt sich also der folgende Satz: bei jeder Z. beschreibt der Leitstrahl in gleichen Zeiten gleiche Flächenräume. Dieses allgemeinste Gesetz der Z. heißt das Prinzip der Erhaltung der Flächen. Dieser sogen. Flächen satz (Flächenprinzip) gilt auch umgekehrt. Wenn ein Körper sich so bewegt, daß der von ihm nach einem Punkte gezogene Leitstrahl in gleichen Zeiten gleiche Flächenräume durchstreicht, so wirkt auf ihn eine stets nach diesem Punkte hin gerichtete Kraft.