Parallaxe

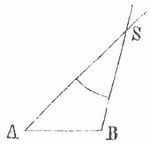
Parallaxe (griech., Abweichung), der Winkel, den zwei von den Standpunkten A und B (Fig. 1) nach dem Punkt S gezogene gerade Linien einschließen, also der Winkel, unter dem die Strecke AB, von S aus gesehen, erscheint. Derselbe ist um so kleiner, je weiter S von A und B entfernt ist. Bewegt man sich von dem Standpunkt A nach B, so dreht sich die Gesichtslinie AS um den Winkel ASB, und wenn hinter S in weiter Ferne ein Hintergrund liegt, so hat es den Anschein, als rückte S auf demselben fort, aber in einer Richtung, die der Bewegung des Beobachters entgegengesetzt ist.

Fig. 1.

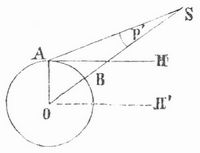
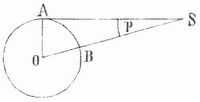
Diese scheinbare Bewegung des Objekts S ist um so stärker, je näher das selbe liegt. Diese Wahrnehmung, die wir an irdischen Gegenständen täglich machen, wiederholt sich auch bei Beobachtung des Mondes und der uns näher stehenden Planeten: sie erscheinen an einer andern Stelle des scheinbaren Himmelsgewölbes, an einem andern scheinbaren Ort, je nach dem Punkte der Erdoberfläche, von dem aus die Beobachtung erfolgt. Infolgedessen werden auch Bedeckungen der Sterne und der Sonne durch den Mond (Sonnenfinsternisse) sowie Vorübergänge des Merkur und der Venus vor der Sonne von verschiedenen Orten der Erdoberfläche aus zu verschiedener Zeit und in verschiedener Weise gesehen. Die astronomischen Tafeln geben aber die geozentrischen Orte der Himmelskörper, d.h. die Orte, an denen sie bei der Beobachtung vom Erdmittelpunkt aus erscheinen würden; um daraus die scheinbaren Orte der Gestirne für jeden Punkt der Erde abzuleiten, bedarf es der Kenntnis der P., d.h. des Winkels, unter dem, von dem betreffenden Himmelskörper aus gesehen, der Erdhalbmesser erscheint. In Fig. 2 ist O der Erdmittelpunkt, der Kreis ein Meridian der Erde, AH der Horizont des Punktes A, OH´ parallel zu AH; der Beobachtungspunkt B liegt so, daß der Stern S im Zenit erscheint, während ihn der Beobachter in A in der Höhe HAS = h erblickt. Der Winkel ASO = p´ ist dann die Höhenparallaxe des Sternes S. Dieselbe erreicht ihren größten Wert, wenn der Stern S für den Punkt A im Horizont steht, wie in Fig. 3, der Winkel ASO = p wird dann die Horizontalparallaxe von S genannt. Durch die P. wird die Höhe eines Sternes vermindert, denn erfolgte in Fig. 2 die Beobachtung des Sternes S von O aus, so daß OH´ parallel AH der Horizont ist, so wäre H´OS = HAS+p´ die Höhe von S. Wenn die P. bekannt ist, so findet man leicht die Entfernung OS = d des Sternes vom Erdmittelpunkt, ausgedrückt in Erdhalbmessern OA = r.

Fig. 2.

Aus Fig. 2 folgt nämlich d = (r.cos h)/sin p´, und aus Fig. 3 ergibt sich d = r/sin p. Wegen der Kleinheit von p´ und p setzt man dafür d = (r.cos h)/p´ = r/p, wo aber p und p´ nicht in Gradmaß, sondern als Bogen, ausgedrückt in Teilen des Halbmessers, anzugeben sind (180° = 3,1415927; 1° = 1/57,296, 1´ = 1/3437,75, 1´´ = 1/206264,8).

Fig. 3.

Aus der Vergleichung der beiden Ausdrücke für d folgt: p´ = p.cos h, d.h. die Höhenparallaxe ist gleich der Horizontalparallaxe, multipliziert mit dem Kosinus der Höhe. Die erstere verschwindet also im Zenit (h = 90°), der scheinbare Ort fällt dann mit dem geozentrischen zusammen. Es wurde bereits erwähnt, daß die Parallaxen der Sterne sehr klein sind. Am größten ist die Horizontalparallaxe des Mondes; sie schwankt zwischen 54 und 61´ und beträgt im Mittel 57´2´´.325, d.h. im Bogenmaß 57,04/3437,7 = 1/60,27, und die mittlere Entfernung des Mondes vom Erdmittelpunkt ist daher 60,27 Erdhalbmesser.

Fig. 4.

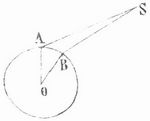
Um die Horizontalparallaxe des Mondes zu finden, beobachtet man an zwei auf demselben Meridian gelegenen Punkten A und B der Erde (Fig. 4) die Kulminationshöhen h u. h´ des Mondmittelpunktes S; ist dann der Winkel AOB oder der Unterschied der geographischen Breiten von A und B bekannt (= w), so ergibt sich der Winkel ASB oder p´´ = h´-h-w, und die Horizontalparallaxe von S ist. p = p´´/(cos h+cos h´). In gleicher Weise läßt sich auch die P. des Mars und der uns am nächsten kommenden Planetoiden zur Zeit der Opposition finden. Die Sonnenparallaxe kann man aber auf diese Weise nicht finden, weil sie viel zu klein ist. Sie beträgt nämlich (nach Newcomb) 8,797´´, d.h. im Bogenmaß 8,797/206264,8 = 1/23400, und die Entfernung der Erde von der Sonne beträgt daher 23,400 Erdhalbmesser, gleich 149,5 Mill. km. Über die Bestimmung dieser wichtigen Größe vgl. Sonne. Die bisher betrachtete P., die scheinbare Größe des Erdhalbmessers für einen Beobachter auf einem Stern, heißt auch die tägliche P. Für genaue Rechnungen ist noch die Abweichung der Erde von der Kugelform in Betracht zu ziehen. Vgl. Brünnow, Lehrbuch der sphärischen Astronomie (4. Aufl., Berl. 1881). Für die Fixsterne ist wegen ihrer großen Entfernung eine tägliche P. nicht bestimmbar; wohl aber kann sich bei den uns am nächsten stehenden Fixsternen eine scheinbare Ortsveränderung zeigen, wenn man sie von zwei einander entgegengesetzten Punkten der Erdbahn, also zu zwei um ¹/₂ Jahr voneinander verschiedenen Zeiten beobachtet. Durch solche Beobachtungen hat man bei einer Anzahl von Fixsternen die jährliche P. gefunden, d.h. den Winkel, unter dem die halbe große Achse der Erdbahn von den betreffenden Fixsternen aus erscheint. Wenn die jährliche P. 1´´, d.h. im Bogenmaß 1/206264,8, beträgt, so ist der Stern 206,264,8 Erdbahnhalbmesser oder Sonnenweiten (zu 149,5 Mill. km) von der Sonne entfernt; das Licht, das nach Michelson in einer Sekunde 299,940 km zurücklegt, braucht für diese Entfernung nahezu 3¹/₄ Jahre. Der uns nächste Fixstern, der also die größte P. hat, ist α Centauri, seine P. beträgt 0,72´´, seine Entfernung 4¹/₂ Lichtjahre. Vgl. Fixsterne, S. 638.