- Harmonische Teilung
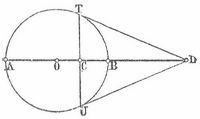
Harmonische Teilung. In der Geometrie wird eine geradlinige Strecke AB von dem zwischen A und B liegenden Punkt C und dem auf der Verlängerung von AB liegenden Punkt D harmonisch geteilt, wenn AB das harmonische Mittel (s. Mittel) zwischen AC und AD ist, also: 2/AB = 1/AC+1/AD. Diese Gleichnn g kann man auch schreiben: AC : CB = AD : BD; also stehen die Entfernungen AC und CB des Punktes C von A und B in demselben Verhältnis wie die Entfernungen AD und BD des Punktes D von A und B, was man auch so ausdrückt: die beiden Punkte C (der innere Teilungspunkt) und D (der äußere Teilungspunkt) teilen beide die Strecke AB in demselben Verhältnis. Ist endlich O die Mitte der Strecke AB, so ist: OA2 = OB2 = OC.OD. So wird z. B. ein Kreisdurchmesser AB (Fig. 1) harmonisch geteilt durch einen beliebigen Punkt D auf seiner Verlängerung und durch den Punkt C, in dem er von der Geraden TU getroffen wird, welche die Berührungspunkte T und U der von D aus an den Kreis gezogenen Tangenten verbindet. Wird die Strecke AB durch C und D harmonisch geteilt, so wird auch die Strecke CD durch A und B harmonisch geteilt, und man sagt ABCD sind vier harmonische Punkte. Vier solche Punkte ABCD ordnen sich dabei immer in zwei Punktepaare AB und CD derart, daß die Punkte des einen Paares die des andern voneinander trennen; die Punkte jedes der beiden Paare heißen zueinander konjugiert, also C ist der konjugierte Punkt zu D, D der konjugierte zu C, B der konjugierte zu A etc.
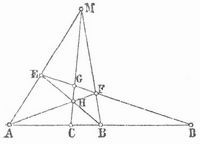
Verbindet man vier harmonische Punkte ABCD mit einem beliebigen Punkt M außerhalb der Geraden A B C D, durch die vier Geraden MA, MB, MC, MD, so erhält man vier harmonische Gerade oder Strahlen; diese werden von jeder beliebigen nicht durch M gehenden Geraden in vier harmonischen Punkten geschnitten. Harmonisches oder vollständiges Vierseit heißt die Figur, die von vier beliebigen Geraden einer Ebene und von deren sechs Schnittpunkten (den Ecken des Vierseits) gebildet wird. Ein solches Vierseit bilden in Fig. 2 die Geraden AF, AM, BE, BM, und A, B, F, E, H, M sind seine Ecken. Zwei Ecken heißen gegenüberliegend, wenn sie nicht derselben Seite angehören, und die Verbindungslinien gegenüberliegender Ecken, also AB, EF und HM, sind die Diagonalen des Vierseits. Jede Diagonale wird nun von den beiden andern harmonisch geteilt, also AB in C und D, EF in G und D, HM in C und G.
Man hat so ein einfaches Mittel, um zu drei Punkten A, B, C einer Geraden den vierten harmonischen D zu konstruieren, und zwar mit dem bloßen Lineal, doch muß man vorher festsetzen, zu welchem der drei Punkte A, B, C der Punkt D konjugiert sein soll. Soll erz. B. zu B konjugiert sein, so muß man ein Vierseit zeichnen, von dem A und C zwei gegenüberliegende Ecken sind und von dem durch B außer der Diagonale AC noch eine zweite Diagonale geht. Die h. T. spielt in der neuern Geometrie eine große Rolle. Vgl. die unter »Geometrie« angeführten Lehrbücher der synthetischen und der projektiven Geometrie.
http://www.zeno.org/Meyers-1905. 1905–1909.