- Pseudoskŏpische Erscheinungen
Pseudoskŏpische Erscheinungen, Täuschungen des Augenmaßes, die unser Urteil über Größe und Gestalt der Gegenstände irre führen. Die Mehrzahl erklärt sich durch vorgefaßte Meinungen, die sich uns unbewußt aufdrängen.
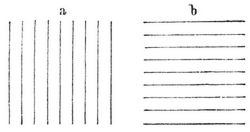
So halten wir z. B. geteilte Größen für ausgedehnter als ununterbrochene, weil wir für die Fülle der wahrgenommenen Einzelheiten unwillkürlich einen größern Raum beanspruchen; die geteilte Hälfte der Geraden (Fig. 1) erscheint uns daher größer und von den beiden gleichen Quadraten der Fig. 2 das vertikal gestreifte breiter, das horizontal gestreifte höher.
Die Entfernung bis zum Horizont halten wir aus demselben Grunde für größer als die bis zum Zenit und schreiben daher dem scheinbaren Himmelsgewölbe die Gestalt einer gedrückten Kuppel zu. Mond und Sonne dünken uns im Horizont entfernter und darum (da der Sehwinkel derselbe ist) größer zu sein,. als wenn sie hoch am Himmel stehen.
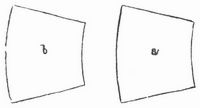
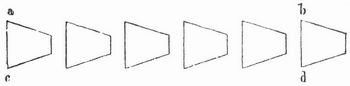
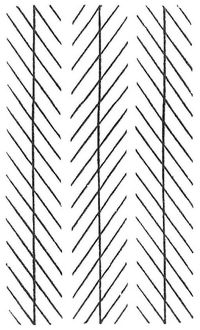
Für eine andre Klasse pseudoskopischer Erscheinungen gibt Fig. 3 ein einfaches Beispiel: von den beiden gleichen Sektoren scheint der nach der Seite der Konvergenz vorliegende a größer zu sein als b, weil wir unwillkürlich nach dieser Seite hin eine Verschmälerung erwarten und dadurch verleitet werden, die vorhandene Breite für größer zu halten, als sie wirklich ist. Diese Täuschung wiederholt sich in der Reihe der Trapeze der Fig. 4, deren Grundlinien a c... b d von a nach b hin scheinbar zunehmen. Denkt man sich daher die Geraden a b und c d gezogen, so scheinen sich dieselben in der Richtung ab voneinander zu entfernen, obgleich sie in Wahrheit parallel sind. Dadurch erklärt sich die Wirkung der Fig. 5 (des Zöllnerschen Musters), die als Wiederholung der Fig. 4 mit Weglassung der parallelen Trapezseiten und Hinzufügung der Geraden a b, c d anzusehen ist.
Auch hier scheinen diese Geraden, obgleich sie in der Tat parallel sind, nach der Seite hin divergent zu sein, nach der die schiefen Querstriche konvergieren. Analog hiermit sind die pseudoskopischen Bewegungserscheinungen; schaut man z. B. von einer Brücke in ein rasch fließendes Gewässer und blickt dann auf die Brücke oder andre ruhende Gegenstände, so scheinen diese sich in entgegengesetzter Richtung zu bewegen. Mit Oppels Amirrheoskop kann man diese Täuschung künstlich hervorrufen. Zu den pseudoskopischen Erscheinungen gehört auch die scheinbare Umkehrung des Reliefs (z. B. einer Medaille, Oppels Anaglyptoskop), die besonders leicht eintritt, wenn die Beleuchtung der vom Beobachter vermuteten entgegengesetzt ist, oder wenn das eine Auge ein solches perspektivisches Bild von einem Gegenstand empfängt, wie es das andre erhalten sollte. Vorrichtungen, die dies durch Prismen oder Spiegel bewirken, heißen Pseudoskope. Vgl. Wundt, Die geometrisch-optischen Täuschungen (Leipz. 1898).
http://www.zeno.org/Meyers-1905. 1905–1909.