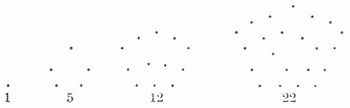
Polygonalzahlen — (v. gr.), die Glieder jeder arithmetischen Reihe (s. Reihe) zweiter Ordnung, deren erstes Glied 1 u. deren zweite (beständige) Differenz eine absolute ganze Zahl ist. Je nachdem die zweite Differenz einer solchen Reihe 1, 2, 3, 4, 5, 6 etc. ist,… … Pierer's Universal-Lexikon
Polygonalzahlen — Polygonalzahlen, die figurierten Zahlen … Universal-Lexikon
Figurat — Figurierte Zahlen sind Klassen von Zahlen, die sich auf geometrische Figuren beziehen. Legt man regelmäßige Figuren aus Spielsteinen und zählt die Steine, erhält man figurierte Zahlen. Beispiele für figurierte Zahlen sind die Quadratzahlen,… … Deutsch Wikipedia
Figurierte Zahl — Figurierte Zahlen sind Klassen von Zahlen, die sich auf geometrische Figuren beziehen. Legt man regelmäßige Figuren aus Spielsteinen und zählt die Steine, erhält man figurierte Zahlen. Beispiele für figurierte Zahlen sind die Quadratzahlen,… … Deutsch Wikipedia
Dreieckszahl — Ein Dreieck aus zehn Steinen Eine Dreieckszahl ist eine Zahl, die der Summe aller Zahlen von 1 bis zu einer Obergrenze n entspricht. Beispielsweise ist die 10 eine Dreieckszahl, da 1 + 2 + 3 + 4 = 10 ist. Die ersten Dreieckszahlen sind 0, 1, 3, 6 … Deutsch Wikipedia
Zentrierte Fünfeckszahl — Die zentrierten Fünfeckszahlen gehören zu den zentrierten Polygonalzahlen, das heißt es sind zweidimensionale Figurierte Zahlen. Sie beziffern die Anzahl von Steinen, mit denen es möglich ist, ein Fünfeck nach dem folgenden Schema auszulegen: Es… … Deutsch Wikipedia
Fermatscher Polygonalzahlensatz — Der fermatsche Polygonalzahlensatz ist ein mathematischer Satz aus der Zahlentheorie. Er besagt, dass jede natürliche Zahl als Summe von höchstens n n Eckszahlen (Polygonalzahlen) darstellbar ist. Ein bekannter Spezialfall ist der Vier Quadrate… … Deutsch Wikipedia
Fünfeckige Pyramidalzahl — In der Mathematik sind Pyramidenzahlen oder Pyramidalzahlen eine Klasse von Polyederzahlen, das heißt dreidimensionale figurierte Zahlen. Von manchen Autoren wird der Begriff Pyramidalzahl für den Spezialfall der quadratischen Pyramidalzahlen… … Deutsch Wikipedia
Pyramidalzahl — In der Mathematik sind Pyramidenzahlen oder Pyramidalzahlen eine Klasse von Polyederzahlen, das heißt dreidimensionale figurierte Zahlen. Von manchen Autoren wird der Begriff Pyramidalzahl für den Spezialfall der quadratischen Pyramidalzahlen… … Deutsch Wikipedia
Pyramidenzahl — In der Mathematik sind Pyramidenzahlen oder Pyramidalzahlen eine Klasse von Polyederzahlen, das heißt dreidimensionale figurierte Zahlen. Von manchen Autoren wird der Begriff Pyramidalzahl für den Spezialfall der quadratischen Pyramidalzahlen… … Deutsch Wikipedia