Goldener Schnitt

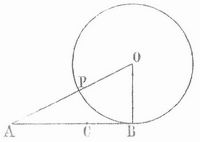
Goldener Schnitt (lat. Sectio aurea), in der Mathematik die Aufgabe, eine gerade Linie AB durch einen Punkt C zwischen A und B in zwei solche Teile zu zerlegen, daß sich der kleinere Teil BC zum größern AC verhält wie der größere zur ganzen Linie AB. Man errichtet zu diesem Zwecke (s. Figur) auf AB in B das Lot BC = ¹/₂ AB, beschreibt um O mit OB als Halbmesser einen Kreis und bestimmt den zwischen A und O liegenden Punkt P, in dem die Gerade AO diesen Kreis trifft, dann ist AC gleich AP. Annähernd ist das Verhältnis des kleinern Teiles BC zum größern AC wie 5:8.

In der Kunst spielen die nach dem Goldenen Schnitt abgenommenen Verhältnisse eine große Rolle, z. B. wählt man bet Fenstern und Türen das Verhältnis der Breite zur Höhe häufig dem Goldenen Schnitt gemäß, ebenso bei Bücherformaten Auch in der Natur findet man das Verhältnis des Goldenen Schnittes sehr häufig Vgl Zeising, Neue Lehre von den Proportionen des menschlichen Körpers (Leipz. 1854) und Der Goldene Schnitt (das. 1884); Wittstein, Der Goldene Schnitt und die Anwendung desselben in der Kunst (Hannov 1874); Matthias. Die Regel vom goldenen Schnitt im Kunstgewerbe (das. 1886). Vgl. auch die Artikel »Mensch« (Darstellung in der bildenden Kunst) und »Viehzucht« (Exterieur).