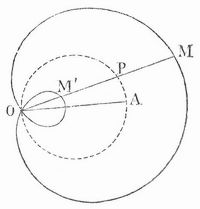
Pascalsche Schnecke

Pascalsche Schnecke

Pascalsche Schnecke, eine Kurve vierten Grades, die man erhält, wenn man durch einen festen Punkt O (s. Figur) auf dem Umfang eines Kreises alle möglichen geraden Linien zieht und von dem Punkte P aus, in dem eine solche Gerade den Kreis zum zweitenmal trifft, auf der betreffenden Geraden jedesmal die Stücke PM = PM´ = b abträgt, wo b eine gegebene Länge ist; der Ort aller so erhaltenen Punkte M, M´ ist eine P. S.

Pascalsche Schnecke.
Pascalsche Schnecke.

Ist b kleiner als der Durchmesser OA des benutzten Kreises, so hat die Kurve wie in der Figur bei O eine Schlinge; wird b gleich OA, so zieht sich diese Schlinge in eine Spitze zusammen, und die Kurve wird eine Kardioide (s. d.); wird b größer als OA, so hat die Kurve an der linken Seite eine Einbuchtung, die aber immer flacher wird, je größer man b wählt. Vgl. Loria, Spezielle ebene Kurven (deutsch von Schütte, Leipz. 1902).


http://www.zeno.org/Meyers-1905. 1905–1909.

Игры ⚽ Поможем сделать НИР

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Pascalsche Schnecke — Die pascalsche Schnecke, auch pascalsche Limaçon, ist eine spezielle ebene Kurve, genauer gesagt eine algebraische Kurve 4. Ordnung. Die Kardioide stellt einen Sonderfall der pascalschen Schnecke dar. Sie ist benannt nach dem französischen… …   Deutsch Wikipedia

  • Schnecke [3] — Schnecke (Pascalsche), die Kurve vierter Ordnung mit der Gleichung (x2 + y2 – b x)2 = a2 (x2 + y2) in rechtwinkligen und r = b cos ± a in Polarkoordinaten. Sie ist zugleich eine Konchoide eines Kreises, d.h. sie entsteht, wenn von einem… …   Lexikon der gesamten Technik

  • Pascals Schnecke — Die pascalsche Schnecke, auch pascalsche Limaçon, ist eine spezielle ebene Kurve, genauer gesagt eine algebraische Kurve 4. Ordnung. Die Kardioide stellt einen Sonderfall der pascalschen Schnecke dar. Sie ist benannt nach dem französischen… …   Deutsch Wikipedia

  • Spinnenlinie — Die pascalsche Schnecke, auch pascalsche Limaçon, ist eine spezielle ebene Kurve, genauer gesagt eine algebraische Kurve 4. Ordnung. Die Kardioide stellt einen Sonderfall der pascalschen Schnecke dar. Sie ist benannt nach dem französischen… …   Deutsch Wikipedia

  • Blaise Pascal — (* 19. Juni 1623 in Clermont Ferrand; † 19. August 1662 in Paris) war ein französischer Mathematiker, Physiker, Literat und katholischer Philosoph …   Deutsch Wikipedia

  • Albrecht Duerer — Selbstbildnis mit Landschaft (Madrider Selbstbildnis), Öl auf Holz (1498), Museo Nacional del Prado, Madrid …   Deutsch Wikipedia

  • Albrecht Duerer der Jüngere — Selbstbildnis mit Landschaft (Madrider Selbstbildnis), Öl auf Holz (1498), Museo Nacional del Prado, Madrid …   Deutsch Wikipedia

  • Albrecht Dürer der Jüngere — Selbstbildnis mit Landschaft (Madrider Selbstbildnis), Öl auf Holz (1498), Museo Nacional del Prado, Madrid …   Deutsch Wikipedia

  • Epizykloiden — Wenn ein Kreis vom Radius a außen auf einem Kreis vom Radius b abrollt, beschreibt ein Punkt auf dem Kreisumfang eine Epizykloide, ein Spezialfall einer Zykloide. Auf diese Weise lassen sich mandalaähnliche Figuren zeichnen, die auch Blumen… …   Deutsch Wikipedia

  • Muschelkurve — Die Konchoide (v. griech. Muschel) ist eine spezielle ebene Kurve. Sie beschreibt die Bewegung eines Punktes, der – von einem festen Punkt (Pol) aus gesehen – zu einer gegebenen Kurve konstanten Abstand einhält. Inhaltsverzeichnis 1 Eigentliche… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”