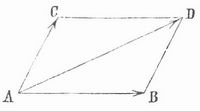
- Parallelogramm der Kräfte
Parallelogramm der Kräfte (und der Bewegungen), der Satz der Mechanik, der lehrt, zwei unter einem Winkel an einem Punkt angreifende Kräfte durch eine einzige Kraft zu ersetzen. Würde die eine Kraft, wenn sie allein wirkte, den Punkt in einer gewissen Zeit von A nach B (s. Figur) treiben, die andre in derselben Zeit von A nach C, so wird derselbe unter gleichzeitiger Einwirkung beider Kräfte den dazwischenliegenden Weg AD durchlaufen, der dargestellt ist durch die von A aus gezogene Diagonale des Parallelogramms, das aus den beiden Wegen AB, AC und dem von ihnen eingeschlossenen Winkel BAC konstruiert werden kann.
Ein Schiff z. B., das durch den Wind allein quer über den Strom von A nach C, durch die Strömung allein in der gleichen Zeit stromabwärts von A nach B getrieben würde, wird durch beide zugleich auf dem Weg AD nach dem weiter stromabwärts gelegenen Punkte D des jenseitigen Ufers gelangen. Da sich die Kräfte ebenso verhalten wie die unter ihrer Einwirkung in gleichen Zeiten zurückgelegten Wege, so kann man dieselbe Konstruktion auch auf die Kräfte selbst anwenden, wenn man sich dieselben ihrem Größenverhältnis und ihrer Richtung nach durch gerade Linien dargestellt denkt. Zwei Kräfte (Seitenkräfte oder Komponenten), die unter irgend einem Winkel an einem Punkt angreifen, können demnach ersetzt werden durch eine resultierende oder Mittelkraft (Resultante, Diagonalkraft), die ihrer Größe und Richtung nach gleich ist der Diagonale des aus den Seitenkräften und dem von ihnen eingeschlossenen Winkel konstruierten Parallelogramms. Um mehrere auf einen Punkt wirkende Kräfte zu einer einzigen Mittelkraft zusammenzusetzen, braucht man nur dieselbe Konstruktion zu wiederholen, indem man die dritte Kraft mit der Mittelkraft aus den beiden ersten, die vierte mit der Mittelkraft aus den drei ersten u. s. s. vereinigt. Bei drei Kräften erhält man so als Resultante die Diagonale des aus ihnen gebildeten Parallelepipeds (Satz vom Parallelepiped der Kräfte). Da CD = AB, kann man den Satz vom P. auch so aussprechen: Setzt man die beiden Komponenten zu einem Winkel aneinander, ohne ihre Richtung zu ändern, so ist die Resultante die Linie, die diesen Winkel zu einem Dreieck ergänzt. Bei beliebig vielen Kräften ist entsprechend die Resultante, die Gerade, welche die aus ihnen zusammengesetzte gebrochene Linie zu einem Polygon ergänzt. (Satz vom Polygon der Kräfte.) Der Satz vom P. lehrt ferner, eine gegebene Kraft (AD) in zwei Seitenkräfte (AB und AC) zu zerlegen, die zusammen dieselbe Wirkung hervorbringen wie jene allein; man braucht nur ein Parallelogramm zu konstruieren, das die gegebene Kraft zur Diagonale hat. Da unzählig viele solcher Parallelogramme möglich sind, so ist die Aufgabe in dieser Allgemeinheit unbestimmt. Damit eine bestimmte Lösung möglich sei, muß entweder 1) eine der beiden Seitenkräfte der Richtung und Größe nach, oder 2) die eine Seitenkraft der Richtung, die andre der Größe nach, oder 3) beide Seitenkräfte der Größe nach, oder endlich 4) beide Seitenkräfte der Richtung nach gegeben sein. Vgl. Westphal, Demonstrationum compositionis virium expositio (Götting. 1817); Jacobi, Praecipuorum inde a Newtono conatuum, compositionem virium demonstrandi, recensio (das. 1818); Matzka, Ein neuer Beweis des Kräftenparallelogramms (Prag 1856).
http://www.zeno.org/Meyers-1905. 1905–1909.